题目内容
19．已知直线l1：（m-2）x-y+5=0与l2：（m-2）x+（3-m）y+2=0平行，则实数m的值为（ ）| A． | 2或4 | B． | 1或4 | C． | 1或2 | D． | 4 |
分析 对m分类讨论，利用两条直线平行的充要条件即可得出．
解答 解：∵l1∥l2，∴m-2=0时，两条直线化为：-y+5=0，y+2=0，此时两条直线平行．
m-2≠0时，$\frac{m-2}{m-2}=\frac{3-m}{-1}$≠$\frac{2}{5}$，解得m=4．
综上可得：m=2或4．
故选：A．
点评 本题考查了两条直线平行的充要条件，考查了分类讨论方法、推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
17．已知sin（α+$\frac{π}{3}$）=sinα，则tanα=（ ）
| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |
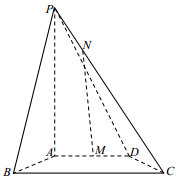如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，BC=2AD=4，AB=CD，∠ABC=60°，N为线段PC上一点，CN=3NP，M为AD的中点．
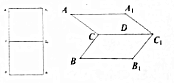已知：矩形AA1B1B，且AB=2AA1=2，C1，C分别是A1B1、AB的中点，D为C1C中点，将矩形AA1B1B沿着直线C1C折成一个60°的二面角，如图所示．
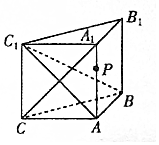如图，侧棱垂直于底面的三棱柱ABC-A1B1C1中，AB⊥AC，AA1+AB+AC=3，AB=AC=t（t＞0），P是侧棱AA1上的动点．
4．已知函数y=f（x）的图象关于直线x=1对称，当x＜1时，f（x）=|（$\frac{1}{2}$）x-1|，那么当x＞1时，函数f（x）的递增区间是（ ）
| A． | （-∞，0） | B． | （1，2） | C． | （2，+∞） | D． | （2，5） |
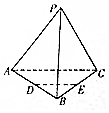如图，在正三棱锥P-ABC中，D，E分别是AB，BC的中点．
9．若集合A={x∈N|5+4x-x2＞0}，B={x|x＜3}，则A∩B等于（ ）
| A． | ∅ | B． | {1，2} | C． | [0，3） | D． | {0，1，2} |