题目内容
17. 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥平面ABC,AC⊥BC,AC=1,BC=2,S,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥平面ABC,AC⊥BC,AC=1,BC=2,S,点D是AB的中点.(I)证明:AC1∥平面CDB1;
(Ⅱ)在线段AB上找一点P,使得直线AC1与CP所成角的为60°,求$\frac{{|{\overrightarrow{AP}}|}}{{|{\overrightarrow{AB}}|}}$的值.
分析 (Ⅰ)设CB1与C1B相交于E,连结DE,证明DE∥AC1,然后证明AC1∥平面CDB1.
(Ⅱ)建立空间直角坐标系,CC1为z轴,CA为x轴,CB为y轴,设$\overrightarrow{AP}=λ\overrightarrow{AB}(0<λ<1)$,利用向量的数量积转化求解即可.
解答 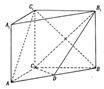 (Ⅰ)证明:设CB1与C1B相交于E,连结DE,….(2分)
(Ⅰ)证明:设CB1与C1B相交于E,连结DE,….(2分)
∵D是AB的中点,E是BC1的中点,∴DE∥AC1,….(6分)
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.….(7分)
(Ⅱ)建立空间直角坐标系,CC1为z轴,CA为x轴,CB为y轴,….(9分)
设$\overrightarrow{AP}=λ\overrightarrow{AB}(0<λ<1)$,
$\overrightarrow{CP}=\overrightarrow{CA}+λ\overrightarrow{AB}=({1-λ,2λ,0})$,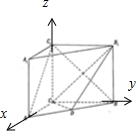
$\overrightarrow{A{C_1}}=({-1,0,1})$
所以$|{cos\left?{\overrightarrow{A{C_1}},\overrightarrow{CP}}\right>}|=\frac{1}{2}$$⇒λ=\frac{1}{3}$
即求$\frac{{|{\overrightarrow{AP}}|}}{{|{\overrightarrow{AB}}|}}$=$\frac{1}{3}$…15分.
(向量写出,夹角公式写出,计算答案错误至少给2分)
非向量做法:指出角给(2分),其他视情况相应给分
点评 本题考查直线与平面平行,点线面距离的求法,异面直线所成角的求法,考查会计信息能力,以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知x1,x2,…,xn的平均数为10,标准差为2,则2x1-1,2x2-1,…,2xn-1的平均数和标准差分别为( )
| A. | 19和2 | B. | 19和3 | C. | 19和4 | D. | 19和8 |
12.定义点P(x0,y0)到直线l:ax+by+c=0(a2+b2≠0)的有向距离为:$d=\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$.已知点P1、P2到直线l的有向距离分别是d1、d2.以下命题正确的是( )
| A. | 若d1=d2=1,则直线P1P2与直线l平行 | |
| B. | 若d1=1,d2=-1,则直线P1P2与直线l垂直 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2≤0,则直线P1P2与直线l相交 |