Question

在△ABC中，I是内心，∠BIC=140°，则∠A的度数是

 

．

Answer 1

考点：圆周角定理

专题：计算题,立体几何

分析：已知I是△ABC的内心，则IB、IC分别平分∠ABC、∠ACB；由三角形内角和定理，可求得∠IBC+∠ICB的度数，也就求出了∠ABC+∠ACB的度数，进而可求出∠BAC的度数．

解答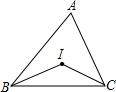： 解：∵点I是△ABC的内心，
∴∠IBC=

1

2

∠ABC，∠ICB=

1

2

∠ACB；
△IBC中，∠BIC=140°；
∴∠IBC+∠ICB=180°-∠BIC=40°；
∴∠ABC+∠ACB=80°；
∴∠BAC=180°-80°=100°．
故答案为：100°．

点评：本题主要考查三角形内切圆的性质以及三角形内角和定理．