题目内容
在各项均为负数的数列{an}中,已知点(an,an+1)(n∈N*)在函数y=2x的图象上,且a2•a5=8.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}的前n项和为Sn,且bn=an+n,求Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}的前n项和为Sn,且bn=an+n,求Sn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由题意可得数列{an}是以2为公比的等比数列,进而求得结论;
(Ⅱ)利用分组求和,由等差数列及等比数列的求和公式求得结论.
(Ⅱ)利用分组求和,由等差数列及等比数列的求和公式求得结论.
解答:
解:(Ⅰ)∵点(an,an+1)(n∈N*)在函数y=2x的图象上,
∴an+1=2an
∴数列{an}是以2为公比的等比数列,
∵数列{an}各项均为负数且a2•a5=8∴a2=-1
∴an=a2•2n-2=-2n-2.
(Ⅱ)由(Ⅰ)得an=-2n-2,
∴bn=an+n=-2n-2+n,
∴sn=b1+b2+…+bn=-(2-1+20+…+2n-2)+(1+2+…+n)=-
+
=
.
∴an+1=2an
∴数列{an}是以2为公比的等比数列,
∵数列{an}各项均为负数且a2•a5=8∴a2=-1
∴an=a2•2n-2=-2n-2.
(Ⅱ)由(Ⅰ)得an=-2n-2,
∴bn=an+n=-2n-2+n,
∴sn=b1+b2+…+bn=-(2-1+20+…+2n-2)+(1+2+…+n)=-
| 2-1(1-2n) |
| 1-2 |
| n(n+1) |
| 2 |
| n2+n+1-2n |
| 2 |
点评:本题主要考查等比数列的定义及等差数列、等比数列的前n项和公式等知识,考查学生的运算求解能力,属基础题.

练习册系列答案
相关题目

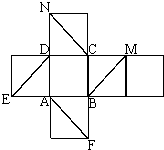 如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是
如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是