题目内容
13．已知tan（π+θ）=-3，求4sin2θ-3sinθcosθ的值．分析 根据根据同角三角函数关系式化简即可．
解答 解：由tan（π+θ）=-3，
可得：tanθ=-3，
那么：4sin2θ-3sinθcosθ=$\frac{4si{n}^{2}θ-3sinθcosθ}{1}$=$\frac{4si{n}^{2}θ-3sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{4ta{n}^{2}θ-3tanθ}{ta{n}^{2}θ+1}$=4.5．
点评 本题主要考察了同角三角函数关系式的应用，属于基本知识的考查．
练习册系列答案
相关题目
10．
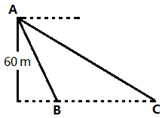如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为60o，30°，此时气球的高是60m，则河流的宽度BC等于（ ）
如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为60o，30°，此时气球的高是60m，则河流的宽度BC等于（ ）| A． | $30\sqrt{3}$ | B． | $30（{\sqrt{3}-1}）$ | C． | $40\sqrt{3}$ | D． | $40（{\sqrt{3}-1}）$ |
1．下列命题中正确的是（ ）
| A． | 若$λ\overrightarrow{a}+μ\overrightarrow{b}$=$\overrightarrow{0}$，则λ=μ=0 | B． | 若$\overrightarrow{a}•\overrightarrow{b}$=0，则$\overrightarrow{a}$∥$\overrightarrow{b}$ | ||
| C． | 若$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$| | D． | 若$\overrightarrow{a}⊥\overrightarrow{b}$，则$\overrightarrow{a}$•$\overrightarrow{b}$=（$\overrightarrow{a}$$•\overrightarrow{b}$）2 |
8．已知抛物线y2=2px（p＞0）与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）有相同的焦点，点A是两曲线的一个公共点，若|AF|=$\frac{5p}{6}$，则椭圆的离心率为（ ）
| A． | $\frac{-5+\sqrt{51}}{2}$ | B． | $\frac{-5+\sqrt{61}}{6}$ | C． | $\frac{1}{2}$ | D． | $\frac{2\sqrt{2}-1}{2}$ |
18．已知集合H={1，2，3，4}，集合K={1，1.5，2，0，-1，-2}，则H∩K为（ ）
| A． | {1，2} | B． | {1，2，0，-1} | C． | （-1，2] | D． | {1.5，0} |
在如图所示的几何体中，AF⊥平面ABCD，EF∥AB，四边形ABCD为矩形，AD=2，AB=AF=2EF=1，P是棱DF的中点．