题目内容
12.已知直线l过点A(-1,0)且与⊙B:x2+y2-2x=0相切于点D,以坐标轴为对称轴的双曲线E过点D,一条渐进线平行于l,则E的方程为( )| A. | $\frac{3{y}^{2}}{4}$-$\frac{{x}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{3{y}^{2}}{2}$=1 | C. | $\frac{5{y}^{2}}{3}$-x2=1 | D. | $\frac{3{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1 |
分析 设直线l:y=k(x+1),求得圆的圆心和半径,运用正弦和圆相切的条件:d=r,求得斜率k,联立直线和圆方程解得交点,求出渐近线方程,设出双曲线方程,代入D的坐标,解方程即可得到所求方程.
解答 解:可设直线l:y=k(x+1),
⊙B:x2+y2-2x=0的圆心为(1,0),半径为1,
由相切的条件可得,d=$\frac{|k+k-0|}{\sqrt{1+{k}^{2}}}$=1,
解得k=±$\frac{\sqrt{3}}{3}$,
直线l的方程为y=±$\frac{\sqrt{3}}{3}$(x+1),
联立x2+y2-2x=0,解得x=$\frac{1}{2}$,y=±$\frac{\sqrt{3}}{2}$,
即D($\frac{1}{2}$,±$\frac{\sqrt{3}}{2}$),
由题意可得渐近线方程为y=±$\frac{\sqrt{3}}{3}$x,
设双曲线的方程为y2-$\frac{1}{3}$x2=m(m≠0),
代入D的坐标,可得m=$\frac{3}{4}$-$\frac{1}{12}$=$\frac{2}{3}$.
则双曲线的方程为$\frac{3{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1.
故选:D.
点评 本题考查直线和圆相切的条件:d=r,双曲线的性质:渐近线,考查联立方程组求交点,以及待定系数法求方程的方法,属于中档题.

练习册系列答案
相关题目
3.在△ABC中,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{DC}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且则$\overrightarrow{AD}$=( )
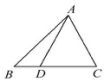

| A. | $\frac{4}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
7.某校从8名教师中选派4名教师去4个边远地区支教,每地1人,其中甲和乙不能同去,甲与丙同去或者同不去,则不同的选派方案的种数是( )
| A. | 240 | B. | 360 | C. | 540 | D. | 600 |
12.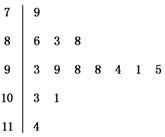 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )| A. | 98 | B. | 94 | C. | 94.5 | D. | 95 |