曲线f(x)=x2-3x+2lnx在x=1处的切线方程为x-y-3=0．题目和参考答案——青夏教育精英家教网——

题目内容

11．曲线f（x）=x²-3x+2lnx在x=1处的切线方程为x-y-3=0．

分析求出函数的导数，计算f（1），f′（1），求出切线方程即可．

解答解：f′（x）=2x-3+$\frac{2}{x}$，
f（1）=-2，f′（1）=1，
故切线方程是：y+2=x-1，
即x-y-3=0，
故答案为：x-y-3=0．

点评本题考查了求切线方程问题，考查导数的应用，是一道基础题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

11．已知条件p：x＞1，条件q：x＞0，则p是q的（　　）条件．

	A．	充要		B．	充分不必要
	C．	必要不充分		D．	既非充分也非必要

12．已知直线l过点A（-1，0）且与⊙B：x²+y²-2x=0相切于点D，以坐标轴为对称轴的双曲线E过点D，一条渐进线平行于l，则E的方程为（　　）

$\frac{3{y}^{2}}{4}$-$\frac{{x}^{2}}{4}$=1

$\frac{{x}^{2}}{2}$-$\frac{3{y}^{2}}{2}$=1

$\frac{5{y}^{2}}{3}$-x²=1

$\frac{3{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1

9．命题“?x＞0，$\sqrt{x}≤x-1$”的否定为?x＞0，$\sqrt{x}＞x-1$．

6．已知函数f（x）=sin（x+$\frac{π}{6}$）-tanα•cosx，且f（$\frac{π}{3}$）=$\frac{1}{2}$．
（1）求tanα的值；
（2）求函数g（x）=f（x）+cosx的对称轴与对称中心．

16．已知等比数列{a_n}中，a₁=2，a₃+2是a₂和a₄的等差中项．
（1）求数列{a_n}的通项公式；
（2）记b_n=na_n，求数列{b_n}的前n项s_n．

3．已知抛物线y²=2px（p＞0）的焦点成F，过点F且倾斜角为45°的直线l与抛物线在第一、第四象限分别交于A、B，则$\frac{|AF|}{|BF|}$等于（　　）

20．若m＜n，p＜q，且（p-m）（p-n）＜0，（q-m）（q-n）＜0，则m，n，p，q从小到大排列顺序是（　　）

1．在正方体ABCD-A₁B₁C₁D₁中，下列几种说法正确的是（　　）

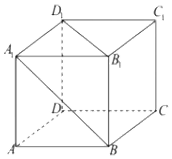
	A．	A₁B∥D₁B		B．	AC₁⊥B₁C
	C．	A₁B与平面DBD₁B₁成角为45°		D．	A₁B，B₁C成角为30°