题目内容
17.若x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≥0\\ x-3≤0\end{array}\right.$则z=x+2y的最小值为3.分析 作出不等式组对应的平面区域,利用z的几何意义即可得到结论.
解答 解:作出不等式组对应的平面区域,
由z=x+2y,得y=$-\frac{1}{2}x+\frac{z}{2}$,平移直线y=$-\frac{1}{2}x+\frac{z}{2}$,由图象可知当直线经过点C时,
直线y=$-\frac{1}{2}x+\frac{z}{2}$的截距最小,此时z最小,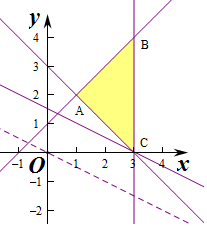
由$\left\{\begin{array}{l}{x-3=0}\\{x+y-3=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$,即C(3,0)
此时z=3+2×0=3.
故答案为:3
点评 本题主要考查线性规划的应用,利用图象平行求得目标函数的最小值,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
相关题目
5.某汽车销售公司同时在甲、乙两地销售一种品牌车,利润(单位:万元)分别为${L_1}=-{x^2}+21x$和L2=2x(其中销售量单位:辆).若该公司在两地一共销售20辆,则能获得的最大利润为( )
| A. | 130万元 | B. | 130.25万元 | C. | 120万元 | D. | 100万元 |
12.已知直线l过点A(-1,0)且与⊙B:x2+y2-2x=0相切于点D,以坐标轴为对称轴的双曲线E过点D,一条渐进线平行于l,则E的方程为( )
| A. | $\frac{3{y}^{2}}{4}$-$\frac{{x}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{3{y}^{2}}{2}$=1 | C. | $\frac{5{y}^{2}}{3}$-x2=1 | D. | $\frac{3{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1 |
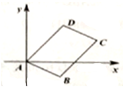 如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.
如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限. 如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.
如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.