题目内容
已知集合A={x|x2-2x<0},B={x|1<x<3},那么A∩B=( )
| A、{x|0<x<2} |
| B、{x|1<x<2} |
| C、{x|0<x<3} |
| D、{x|1<x<3} |
考点:交集及其运算
专题:集合
分析:根据集合的交集运算进行即可即可.
解答:
解:∵A={x|x2-2x<0}={x|0<x<2},B={x|1<x<3},
∴A∩B={x|1<x<2},
故选:B
∴A∩B={x|1<x<2},
故选:B
点评:本题主要考查集合的基本运算,比较基础.

练习册系列答案
相关题目
“m=3”是“f(x)=xm为(0,+∞)上的增函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=(1,2),(
+
)∥
,则
可以为( )
| a |
| a |
| b |
| b |
| b |
| A、(1,2) |
| B、(1,-2) |
| C、(2,1) |
| D、(2,-1) |
已知角θ的顶点坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,则
=( )
sin(
| ||
sin(
|
A、-
| ||||
B、0或
| ||||
C、
| ||||
D、
|
已知全集U=R,集合 A={x|-2≤x≤3},B={x|x>4或x<-1},那么 A∩B=( )
| A、{x|-2≤x<4} |
| B、{x|-2≤x<-1} |
| C、{x|x≤3或x≥4} |
| D、{x|-1≤x≤3} |
已知集合A={x|x=2k+1,k∈Z},B={x|
≥0},则A∩B=( )
| 1+x |
| 3-x |
| A、[-1,3] |
| B、{-1,1,3} |
| C、[-1,1] |
| D、{-1,1} |
使函数y=2sin(2x+φ+
)为奇函数,且在[0,
]上是减函数的φ的一个值是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
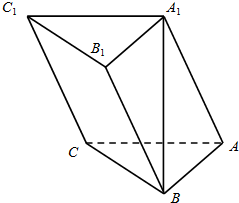 在三棱柱ABC-A1B1C1中,AB⊥AC,A1B⊥平面ABC,且AB=AC=A1B=2.
在三棱柱ABC-A1B1C1中,AB⊥AC,A1B⊥平面ABC,且AB=AC=A1B=2.