题目内容
x,y满足
+
=1(1≤x≤3).
(1)求
的最值;
(2)求
的最值.
| x |
| 3 |
| y |
| 4 |
(1)求
| y |
| x |
(2)求
| y-4 |
| x-3 |
考点:直线的截距式方程
专题:直线与圆
分析:(1)如图所示,设
=k,B(1,
).则kOA≤k≤kOB,利用斜率计算公式即可得出.
(2)
表示线段AB上的点与点P(3,4)连线的直线的斜率.可得k≥kPB.
| y |
| x |
| 8 |
| 3 |
(2)
| y-4 |
| x-3 |
解答:
解:(1)如图所示,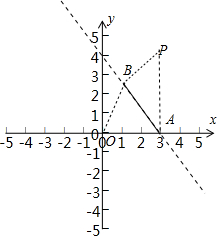
设
=k,B(1,
).
则kOA=0,kOB=
=
.
则kOA≤k≤kOB,
∴0≤k≤
.
∴
的最大值、最小值分别为:
,0;
(2)
表示线段AB上的点与点P(3,4)连线的直线的斜率.
∴k≥kPB=
=
.
∴
≥
,其最小值为
,无最大值.
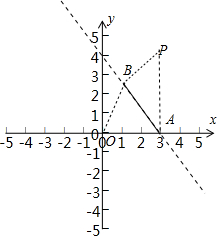
设
| y |
| x |
| 8 |
| 3 |
则kOA=0,kOB=
| ||
| 1 |
| 8 |
| 3 |
则kOA≤k≤kOB,
∴0≤k≤
| 8 |
| 3 |
∴
| y |
| x |
| 8 |
| 3 |
(2)
| y-4 |
| x-3 |
∴k≥kPB=
4-
| ||
| 3-1 |
| 2 |
| 3 |
∴
| y-4 |
| x-3 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查了直线的斜率计算公式、数形结合思想方法,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若m,n是不同的直线,α,β是不同的平面,则下列命题中,错误的是( )
| A、若m⊥α,n⊥α,则m∥n |
| B、若m?α,α∥β,则m∥β |
| C、若m∥α,n∥α,则m∥n |
| D、若m∥n,m∥α,n?α,则n∥α |
函数f(x)=2sin2(
-x)-1(x∈R)是( )
| π |
| 4 |
| A、最小正周期为2π的奇函数 |
| B、最小正周期为π的奇函数 |
| C、最小正周期为π的偶函数 |
| D、最小正周期为2π的偶函数 |
函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(x)>0的解集为( )
| A、{x|x<0或x>4} |
| B、{x|-2<x<2} |
| C、{x|x>2或x<-2} |
| D、{x|0<x<4} |
已知集合A={x|x2-2x<0},B={x|1<x<3},那么A∩B=( )
| A、{x|0<x<2} |
| B、{x|1<x<2} |
| C、{x|0<x<3} |
| D、{x|1<x<3} |