题目内容
已知椭圆C:
+
=1(a>b>0),离心率为
,两焦点分别为F1、F2,过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
(1)求椭圆C的方程;
(2)过点P(m,0)作圆x2+y2=1的切线l交椭圆C于A,B两点,求弦长|AB|的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)过点P(m,0)作圆x2+y2=1的切线l交椭圆C于A,B两点,求弦长|AB|的最大值.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)利用已知条件求出椭圆方程中的几何量,即可求椭圆C的方程;
(2)利用直线的斜率存在与不存在,分别与椭圆方程联立,利用韦达定理,以及弦长公式表示弦长|AB|通过基本不等式求解弦长的最大值.
(2)利用直线的斜率存在与不存在,分别与椭圆方程联立,利用韦达定理,以及弦长公式表示弦长|AB|通过基本不等式求解弦长的最大值.
解答:
解:(1)由题得:
=
,4a=8,所以a=2,c=
. …(3分)
又b2=a2-c2,所以b=1即椭圆C的方程为
+y2=1.…(4分)
(2)由题意知,|m|≥1.
当m=1时,切线l的方程x=1,点A、B的坐标分别为(1,
),(1,-
),
此时|AB|=
; 当m=-1时,同理可得|AB|=
…(5分)
当|m|>1时,设切线l的方程为y=k(x-m),(k≠0)
由
得(1+4
)
-8k2mx+4k2m2-4=0
设A、B两点的坐标分别为(x1,y1),(x2,y2),
则△=64k4m2-16(1+4k2)(4k2m2-4)=48k2>0x1+x2=
,x1x2=
又由l与圆
+
=1相切,得
=1,即m2k2=k2+1.得k2=
所以|AB|=
=
=
…(9分)
因为|m|≥1所以|AB|=
=
≤2,
且当m=±
时,|AB|=2,
由于当m=±1时,|AB|=
,所以|AB|的最大值为2.…(12分)
| c |
| a |
| ||
| 2 |
| 3 |
又b2=a2-c2,所以b=1即椭圆C的方程为
| x2 |
| 4 |
(2)由题意知,|m|≥1.
当m=1时,切线l的方程x=1,点A、B的坐标分别为(1,
| ||
| 2 |
| ||
| 2 |
此时|AB|=
| 3 |
| 3 |
当|m|>1时,设切线l的方程为y=k(x-m),(k≠0)
由
|
| k | 2 |
| x | 2 |
设A、B两点的坐标分别为(x1,y1),(x2,y2),
则△=64k4m2-16(1+4k2)(4k2m2-4)=48k2>0x1+x2=
8
| ||
| 1+4k2 |
| 4k2m2-4 |
| 1+4k2 |
又由l与圆
| x | 2 |
| y | 2 |
| |km| | ||||
|
| 1 |
| m2-1 |
所以|AB|=
(x2-x1
|
(1+
|
4
| ||
|
因为|m|≥1所以|AB|=
4
| ||
|
4
| ||
|m|+
|
且当m=±
| 3 |
由于当m=±1时,|AB|=
| 3 |
点评:本题考查椭圆的方程的求法,直线与椭圆的位置关系,弦长公式的应用,考查分析问题解决问题的能力以及转化思想的应用.

练习册系列答案
相关题目
已知a>0,若不等式|x-a|+3x≤0的解集为{x|x≤-1},则a的值为( )
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
如图,△AOB是一个水平放置的平面图形的直观图,则其平面图形的面积为( )
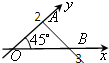

| A、3 | ||||
| B、6 | ||||
C、3
| ||||
D、
|
函数y=mx2m-n的导数为y′=4x3,则( )
| A、m=-1,n=-2 |
| B、m=-1,n=2 |
| C、m=1,n=2 |
| D、m=1,n=-2 |
当点(x,y)在直线x+3y=2上移动时,u=3x+27y+1的最小值是( )
| A、7 | |||
B、3
| |||
C、1+2
| |||
| D、6 |
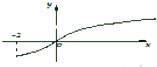 已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为
已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为