题目内容
函数y=mx2m-n的导数为y′=4x3，则（ ）
| A、m=-1，n=-2 |
| B、m=-1，n=2 |
| C、m=1，n=2 |
| D、m=1，n=-2 |
考点：导数的运算
专题：导数的概念及应用
分析：已知函数y=mx2m-n根据幂函数的求导法则对其进行求导，再根据y'=4x3，进行求解；
解答：
解：∵函数y=mx2m-n，
∴y′=m（2m-n）x2m-n-1，
又∵y'=4x3，
∴m（2m-n）=4，2m-n-1=3，解得m=1，n=-2．
故选D．
∴y′=m（2m-n）x2m-n-1，
又∵y'=4x3，
∴m（2m-n）=4，2m-n-1=3，解得m=1，n=-2．
故选D．
点评：本题主要考查导数的运算，主要是幂函数的求导，是一道基础题．
练习册系列答案
相关题目
已知a，b，c为△ABC的三个内角A，B，C的对边，向量
=（
，-1），
=（sinA，cosA）．若
⊥
，且acosB+bcosA=csinc，则角A，B的大小分别为（ ）
| m |
| 3 |
| n |
| m |
| n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
复数
的虚部为（ ）
| 1+2i |
| 2+i |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中为真命题的是（ ）
| A、第一象限的角一定是锐角 |
| B、终边相同的角一定相等 |
| C、相等的角，终边一定相同 |
| D、小于90°的角一定是锐角 |
当-
≤x≤
时，函数y=sin x+
cos x的最大值和最小值分别为（ ）
| π |
| 3 |
| π |
| 3 |
| 3 |
| A、1，-1 | ||
B、1，-
| ||
C、2，
| ||
| D、2，0 |
某几何体的三视图如图所示，当a+b取最大值时，这个几何体的体积为（ ）
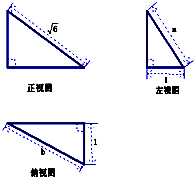
A、
| ||
B、
| ||
C、
| ||
D、
|