题目内容
下列函数中既不是奇函数也不是偶函数的是( )
| A、y=2|x| | ||||
B、y=lg(
| ||||
| C、y=2x-2-x | ||||
D、
|
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:由函数奇偶性的定义,首先观察定义域是否关于原点对称,再计算f(-x),与f(x)比较,对选项加以判断即可.
解答:
解:对于A.有f(-x)=2|-x|=f(x),则为偶函数,不满足条件;
对于B.有
>x,解得x∈R,即定义域关于原点对称,
且有f(-x)+f(x)=lg(
+x)+lg(
-x)=lg(1+x2-x2)=0,
即有f(x)为奇函数,则不满足条件;
对于C.定义域R关于原点对称,且有f(-x)+f(x)=2-x-2x+2x-2-x=0,则为奇函数,不满足条件;
对于D.定义域R关于原点对称,但f(-x)=
-
x≠f(x),且≠-f(x),
则既不是奇函数,也不是偶函数,满足条件.
故选D.
对于B.有
| 1+x2 |
且有f(-x)+f(x)=lg(
| 1+x2 |
| 1+x2 |
即有f(x)为奇函数,则不满足条件;
对于C.定义域R关于原点对称,且有f(-x)+f(x)=2-x-2x+2x-2-x=0,则为奇函数,不满足条件;
对于D.定义域R关于原点对称,但f(-x)=
| 3 |
| 5 |
| 4 |
| 5 |
则既不是奇函数,也不是偶函数,满足条件.
故选D.
点评:本题考查函数的奇偶性的判断,注意首先观察定义域是否关于原点对称,再计算f(-x),与f(x)比较,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知R是实数集,集合P={x|y=ln(x2+2014x-2015)},Q={y|y=
},则(∁RP)∪Q( )
| -x2+2x+3 |
| A、(0,1] |
| B、[0,1] |
| C、(-2015,1] |
| D、[-2015,2] |

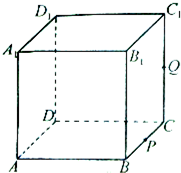 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是