Question

16．某市某小学学生的体重平均值知下表：

身高/cm	60	70	80	90	100	110
体重/kg	6.13	7.90	9.99	12.15	15.02	17.50
身高/cm	120	130	140	150	160	170
体重/kg	20.02	26.86	31.11	38.85	47.25	55.05

（1）根据该表提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个学校学生体重y（kg）与身高x（cm）的函数关系？结合以下所供参考数据，选择适当两组数据，试写出这个函数模型的解析式．（供选择的函数模型：①y=ax${\;}^{\frac{1}{2}}$+b，②y=a•b²，③y=，a（lgx）+b）．
（2）若体重超过相同身高体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么该校某一学生的身高为175cm，体重为78kg，他的体重是否正常？
供参考数据：5.98$\frac{1}{90}$≈1.02，8.98${\;}^{\frac{1}{110}}$≈1.02，1.02⁶⁰≈3.28，1.02⁷⁰≈4.00，1.02¹⁶⁰≈23.77，1.02¹⁷⁰≈28.98，1.02¹⁷⁵≈31.99．

Answer 1

分析 （1）根据表中数据画出散点图，观察发现，这些点的连线是一条向上弯曲的曲线，根据这些点的分布情况，可以考虑用y=a•b^x这一函数模型来近似刻画这个地区未成年男性体重y与身高x的函数关系．
2）将x=175代入y=2×1.02^x得y=2×1.02¹⁷⁵，由计算器可算得y≈63.98，即可得出结论．

解答 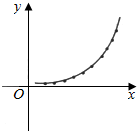解：（1）以身高为横坐标，体重为纵坐标，画出散点图如图所示，根据点的分布情况，可考虑以y=a•b^x作为刻画这个地区未成年男性的体重与身高关系的函数模型．不妨取其中的两组数据（70，7.90），（160，47.25）代入y=a•b^x，得7.90=a•b⁷⁰，47.25=a•b¹⁶⁰，用计算器可算得a≈2，b≈1.02．
∴得到一个函数模型为y=2×1.02^x，作出上述函数的图象（图略）之后．可以发现，这个函数模型与已知数据的拟合程度较好，这说明它能较好地反映这个地区未成年男性体重与身高的关系
（2）将x=175代入y=2×1.02^x得y=2×1.02¹⁷⁵，
由计算器可算得y≈63.98，
由于78÷63.98≈1.22＞1.2，所以，这个男性体型偏胖．

点评 本题的解题过程，体现了根据收集到的数据的特点，通过建立函数模型，解决实际问题的基本过程．