题目内容
20.某三棱锥的三视图如图所示,则该几何体的体积为$\frac{4}{3}$.
分析 几何体为三棱锥,底面为俯视图三角形,棱锥的高为1,代入体积公式计算即可.
解答 解:由三视图可知几何体为三棱锥,底面为俯视图三角形,底面积S=$\frac{1}{2}×4×2$=4,棱锥的高为h=1,
∴棱锥的体积V=$\frac{1}{3}$Sh=$\frac{1}{3}×4×1$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了棱锥的三视图和体积计算,是基础题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
16.某市某小学学生的体重平均值知下表:
(1)根据该表提供的数据,能否建立恰当的函数模型,使它能比较近似地反映这个学校学生体重y(kg)与身高x(cm)的函数关系?结合以下所供参考数据,选择适当两组数据,试写出这个函数模型的解析式.(供选择的函数模型:①y=ax${\;}^{\frac{1}{2}}$+b,②y=a•b2,③y=,a(lgx)+b).
(2)若体重超过相同身高体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么该校某一学生的身高为175cm,体重为78kg,他的体重是否正常?
供参考数据:5.98$\frac{1}{90}$≈1.02,8.98${\;}^{\frac{1}{110}}$≈1.02,1.0260≈3.28,1.0270≈4.00,1.02160≈23.77,1.02170≈28.98,1.02175≈31.99.
| 身高/cm | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重/kg | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 |
| 身高/cm | 120 | 130 | 140 | 150 | 160 | 170 |
| 体重/kg | 20.02 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
(2)若体重超过相同身高体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么该校某一学生的身高为175cm,体重为78kg,他的体重是否正常?
供参考数据:5.98$\frac{1}{90}$≈1.02,8.98${\;}^{\frac{1}{110}}$≈1.02,1.0260≈3.28,1.0270≈4.00,1.02160≈23.77,1.02170≈28.98,1.02175≈31.99.
5.长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,则BD1与平面ABCD所成的角的大小是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.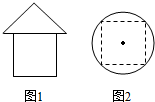 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )| A. | $2\sqrt{2}π+20$ | B. | $\frac{{2\sqrt{2}π}}{3}+8$ | C. | $({2\sqrt{2}+2})π+16$ | D. | $2\sqrt{2}π+16$ |
9.设集合A={x|x2-3x-4>0},集合B={x|-2<x<5},则A∩B=( )
| A. | {x|-1<x<4} | B. | {x|-2<x<-1或4<x<5} | C. | {x|x<-1或x>4} | D. | {x|-2<x<5} |
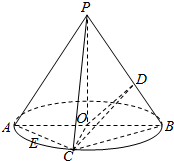 在如图所示的圆锥中,PO是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB上一点,且PO=2,OB=1.
在如图所示的圆锥中,PO是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB上一点,且PO=2,OB=1.