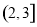题目内容
6.△ABC的顶点为A(1,3),B(-1,2)和C(4,1),求cosC.分析 由题意和距离公式分别可得三角形的三边,由余弦定理可得.
解答 解:∵△ABC的顶点为A(1,3),B(-1,2)和C(4,1),
∴a=BC=$\sqrt{(-1-4)^{2}+(2-1)^{2}}$=$\sqrt{26}$,
b=AC=$\sqrt{(1-4)^{2}+(3-1)^{2}}$=$\sqrt{13}$,
c=AB=$\sqrt{(-1-1)^{2}+(2-3)^{2}}$=$\sqrt{5}$,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{35\sqrt{2}}{52}$
点评 本题考查余弦定理,涉及两点间的距离公式,属基础题.

练习册系列答案
相关题目
14.在区间(-1,+∞)内,函数y=ex-x是( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减 | D. | 先减后增 |
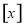 表示不超过
表示不超过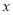 的最大整数,如
的最大整数,如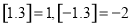 .设函数
.设函数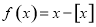 ,若方程
,若方程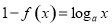 有且仅有3个实数根,则正实数
有且仅有3个实数根,则正实数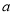 的取值范围为( )
的取值范围为( )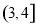 B.
B.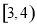 C.
C. D.
D.