题目内容
15.已知{an}是等差数列,a1=2,a3+a6+a9=36.数列{bn-an}的前n项和为Sn,且Sn+1=2Sn+2(n∈N*),b1=4(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项的和.
分析 (1)由已知求出等差数列的公差,可得数列{an}的通项公式,再由Sn+1=2Sn+2,利用构造等比数列求得Sn,再由数列{bn-an}的前n项和为Sn,结合数列的分组求和可得{bn}的前n项和,进而求得{bn}的通项公式;
(2)直接由(1)可得数列{bn}的前n项的和.
解答 解:(1)设等差数列{an}的公差为d,由a3+a6+a9=36,
得3a6=36,a6=12,
又a1=2,∴$d=\frac{{a}_{6}-{a}_{1}}{6-1}=\frac{12-2}{5}=2$,
∴an=a1+(n-1)d=2+2(n-1)=2n.
再由Sn+1=2Sn+2,得Sn+1+2=2(Sn+2),
∴数列{Sn+2}是以S1=b1-a1=4-2=2为首项,以2为公比的等比数列,
则${S}_{n}+2={2}^{n}$,
∴${S}_{n}={2}^{n}-2$.
则(b1-a1)+(b2-a2)+…+(bn-an)=(b1+b2+…+bn)-(a1+a2+…+an)
=(b1+b2+…+bn)-(2n+$\frac{n(n-1)×2}{2}$)=(b1+b2+…+bn)-(n2+n)=2n-2.
∴b1+b2+…+bn=2n+n2+n-2.
则当n≥2时,bn=2n+n2+n-2-2n-1-(n-1)2-(n-1)+2=2n-1+2n.
验证b1=4不适合上式.
∴${b}_{n}=\left\{\begin{array}{l}{4,n=1}\\{{2}^{n-1}+2n,n≥2}\end{array}\right.$;
(2)由(1)可知,数列{bn}的前n项的和Tn=b1+b2+…+bn=2n+n2+n-2.
点评 本题考查等差数列的通项公式,考查了等差数列的前n项和,考查数列的分组求和,关键是掌握对于任意数列{an},都有an=Sn-Sn-1(n≥2),是中档题.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案 如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和.
如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和.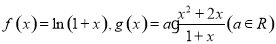 .
.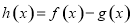 在定义域内单调递减,求
在定义域内单调递减,求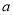 的取值范围;
的取值范围;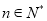 ,证明:
,证明: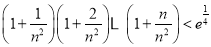 (
(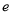 为自然对数的底数).
为自然对数的底数).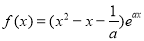 (
(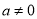 ).
).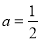 时,求函数
时,求函数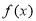 的零点;
的零点;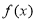 的单调区间;
的单调区间;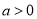 时,若
时,若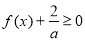 对
对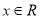 恒成立,求
恒成立,求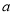 的取值范围.
的取值范围.