题目内容
18.若cosθ<$\frac{\sqrt{3}}{2}$,sinθ>-$\frac{\sqrt{3}}{2}$,写出角θ的取值范围.分析 由题意根据正弦函数,余弦函数的图象和性质即可得解.
解答 解:∵cosθ<$\frac{\sqrt{3}}{2}$,
∴2kπ+$\frac{π}{6}$<θ<2kπ+$\frac{11π}{6}$,k∈Z,
∵sinθ>-$\frac{\sqrt{3}}{2}$,
∴2kπ<θ<2kπ+$\frac{4π}{3}$,2kπ+$\frac{5π}{3}$<θ<2kπ+2π,k∈Z,
∴角θ的取值范围是:(2kπ+$\frac{π}{6}$,2kπ+$\frac{4π}{3}$)∪(2kπ+$\frac{5π}{3}$,2kπ+$\frac{11π}{6}$),k∈Z.
点评 本题主要考查正弦函数,余弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
8.已知数列{an}的前n项和Sn=n2-2n+1,△ABC的三边长之比为a3:a4:a5,则△ABC的最大角的余弦值为( )
| A. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{\sqrt{3}}{2}$ |
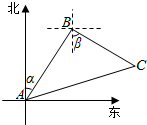 如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和.
如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和.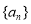 的前
的前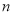 项和为
项和为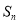 ,若
,若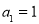 ,且
,且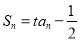 ,其中
,其中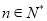 .
.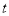 的值和数列
的值和数列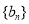 满足
满足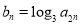 ,求数列
,求数列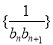 的前
的前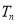 .
.