题目内容
已知向量
=(sinx,cos2x-
),
=(cosx,-
),其中x∈R,函数f(x)=5
•
-3
(1)求函数f(x)的最小正周期;
(2)确定函数f(x)的单调区间;
(3)函数f(x)的图象可以由函数y=5sin2x的图象经过怎样的变化而得到?
| a |
| 1 |
| 2 |
| b |
| 3 |
| a |
| b |
(1)求函数f(x)的最小正周期;
(2)确定函数f(x)的单调区间;
(3)函数f(x)的图象可以由函数y=5sin2x的图象经过怎样的变化而得到?
考点:三角函数中的恒等变换应用,数量积的坐标表达式
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(1)先化简求f(x)的解析式,根据周期公式可求函数f(x)的最小正周期;
(2)由三角函数的图象与性质可求得函数f(x)的单调区间;
(3)先左移
个单位,再向下平移3个单位可得到函数y=5sin2x的图象.
(2)由三角函数的图象与性质可求得函数f(x)的单调区间;
(3)先左移
| π |
| 6 |
解答:
解:f(x)=5
•
-3=5sinxcosx+5(cos2x-
)•(-
)-3
=5sinxcosx-5
cos2x+
-3=
sin2x-5
•
+
-3
=
sin2x-
cos2x-3=5sin(2x-
)-3…(4分)
(1)由周期公式可求得:T=
=π…(6分)
(2)令2kπ-
≤2x-
≤2kπ+
,(k∈Z),从而可解得函数f(x)的递增区间:[kπ-
,kπ+
π](k∈z)
令2kπ+
≤2x-
≤2kπ+
,(k∈Z),从而可解得函数f(x)的递减区间:[kπ+
π,kπ+
π](k∈z)…(10分)
(3)先左移
个单位可得到函数y=5sin[2(x+
)-
]-3的图象,再向下平移3个单位可得到函数y=5sin[2(x+
)-
]=5sin2x的图象 …(12分)
| a |
| b |
| 1 |
| 2 |
| 3 |
=5sinxcosx-5
| 3 |
5
| ||
| 2 |
| 5 |
| 2 |
| 3 |
| 1+cos2x |
| 2 |
5
| ||
| 2 |
=
| 5 |
| 2 |
5
| ||
| 2 |
| π |
| 3 |
(1)由周期公式可求得:T=
| 2π |
| 2 |
(2)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5 |
| 12 |
令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5 |
| 12 |
| 11 |
| 12 |
(3)先左移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
点评:本题主要考察了三角函数的图象与性质,平面向量及应用,属于基本知识的考查.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知i为虚数单位,且,则|
|=
实数a的值为( )
| 1+ai |
| 2i |
| ||
| 2 |
| A、1 | B、2 |
| C、1或-1 | D、2或-2 |
sinα=
,α∈(
,π),则cos(
-α)=( )
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中,既是奇函数又是减函数的是( )
| A、y=x2,x∈R |
| B、y=-x3,x∈R |
| C、y=2x,x∈R |
| D、y=2x,x∈R |
设集合A={x|x=2k-1,k∈Z},则( )
| A、3∈A | B、3∉A |
| C、3⊆A | D、3?A |
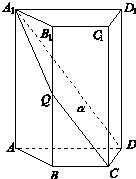 如图,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.