题目内容
19.已知($\frac{1}{x}$+y)(x+$\frac{a}{y}$)5的展开式中$\frac{{x}^{2}}{{y}^{2}}$的系数为20a,其中a≠0,则a的值为-2或1.分析 把(x+$\frac{a}{y}$)5 按照二项式定理展开,可得已知($\frac{1}{x}$+y)(x+$\frac{a}{y}$)5的展开式中$\frac{{x}^{2}}{{y}^{2}}$的系数,再根据中$\frac{{x}^{2}}{{y}^{2}}$的系数为20a,求得a的值.
解答 解:($\frac{1}{x}$+y)(a+$\frac{a}{y}$)5=($\frac{1}{x}$+y)(${C}_{5}^{0}$•x5+${C}_{5}^{1}$•x4•$\frac{a}{y}$+${C}_{5}^{2}$•x3•${(\frac{a}{y})}^{2}$+${C}_{5}^{3}$•x2•${(\frac{a}{y})}^{3}$+${C}_{5}^{4}$•ax${(\frac{a}{y})}^{4}$+${C}_{5}^{5}$•${(\frac{a}{y})}^{5}$),
故($\frac{1}{x}$+y)(a+$\frac{a}{y}$)5的展开式中$\frac{{x}^{2}}{{y}^{2}}$的系数为${C}_{5}^{2}$•a2+${C}_{5}^{3}$•a3=20a,
即a2+a-2=0,求得a=-2或a=1,
故答案为:-2或1.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
14.执行如图的程序框图,如果输入的N=10,则输出的x=( )
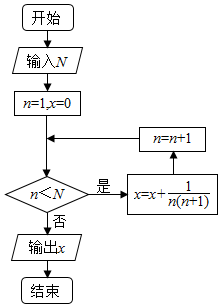

| A. | 0.5 | B. | 0.8 | C. | 0.9 | D. | 1 |
4.直线x+(l-m)y+3=0(m为实数)恒过定点( )
| A. | (3,0) | B. | (0,-3) | C. | (-3,0) | D. | (-3,1) |
11.若复数z满足z(1-i)=|1-i|+i,则z的实部为( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | 1 | D. | $\frac{\sqrt{2}+1}{2}$ |
8.已知b为如图所示的程序框图的输出结果,则b=( )


| A. | 9 | B. | 7 | C. | 5 | D. | 4 |