题目内容
4.直线x+(l-m)y+3=0(m为实数)恒过定点( )| A. | (3,0) | B. | (0,-3) | C. | (-3,0) | D. | (-3,1) |
分析 令$\left\{\begin{array}{l}{x+3=0}\\{(1-m)y=0}\end{array}\right.$,可得直线恒过定点的坐标.
解答 解:方程化为:(x+3)+(1-m)y=0,
令$\left\{\begin{array}{l}{x+3=0}\\{(1-m)y=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-3}\\{y=0}\end{array}\right.$,
故直线恒过定点(-3,0),
故选:C.
点评 本题考查了直线系的应用,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
15.执行如图所示的程序框图,若输入n=10,则输出的S=( )
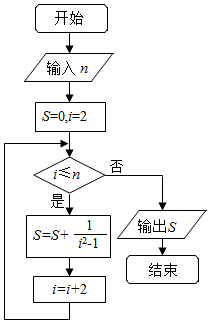

| A. | $\frac{5}{11}$ | B. | $\frac{20}{21}$ | C. | $\frac{10}{21}$ | D. | $\frac{10}{11}$ |
12.在中秋节前,小雨的妈妈买来5种水果,4种肉类食品做月饼.要求每种馅只能用两种食材,且水果和肉类不能混合在一起做馅,则小雨妈妈做出水果馅月饼的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{9}$ |
16.命题“?x∈[-2,+∞),x+3≥l“的否定为( )
| A. | ?x0[-2,+∞),x0+3<1 | B. | ?x0[-2,+∞),x0+3≥l | C. | ?x∈[-2,+∞),x+3<1 | D. | ?x∈(-∞,-2),x+3≥l |
13.执行如图所示的程序框图,则输出结果a的值为( )


| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -1 |
14.已知正项数列{an}中,a1=l,a2=2,$2a_{n}^2=a_{n+1}^2+a_{n-1}^2$(n≥2),则a6=( )
| A. | 16 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 45 |