题目内容
14.执行如图的程序框图,如果输入的N=10,则输出的x=( )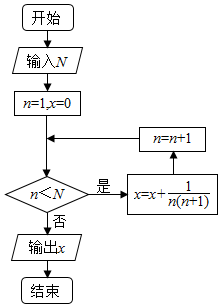
| A. | 0.5 | B. | 0.8 | C. | 0.9 | D. | 1 |
分析 执行程序框图,写出每一次循环x,n的值,当有n=10,n<N不成立,从而输出S的值,用裂项法求和即可得解.
解答 解:执行程序框图,有
N=10,n=1,x=0
满足条件n<10,x=$\frac{1}{1×2}$,n=2
满足条件n<10,x=$\frac{1}{1×2}$+$\frac{1}{2×3}$,n=3
…
满足条件n<10,x=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{9×10}$,n=10
不满足条件n<10,退出循环,输出x═$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{9×10}$=(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{9}$-$\frac{1}{10}$)=1-$\frac{1}{10}$=0.9.
故选:C.
点评 本题主要考察程序框图和算法,考查了用裂项法求数列的和,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.△ABC中,∠C=90°,AC=4,BC=3,D是AB的中点,E,F分别是边BC、AC上的动点,且EF=1,则$\overrightarrow{DE}$$•\overrightarrow{DF}$的最小值等于( )
| A. | $\frac{\sqrt{5}}{4}$ | B. | $\frac{15}{4}$ | C. | $\frac{17}{4}$ | D. | $\frac{\sqrt{17}}{4}$ |
5.执行如图的程序框图(n∈N*),则输出的S=( )
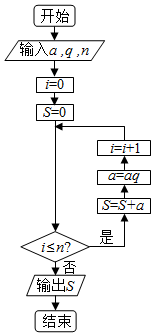

| A. | a+aq+…+aqn-1 | B. | $\frac{{a(1-{q^n})}}{1-q}$ | C. | a+aq+…+aqn | D. | $\frac{{a(1-{q^{n+1}})}}{1-q}$ |
6.执行如图所示的程序框图,若输出的n=7,则输入的整数K的最大值是( )


| A. | 18 | B. | 50 | C. | 78 | D. | 306 |