题目内容
10.在△ABC中,角A,B,C的对边分别是a,b,c,已知asinA+bsinB-csinC=$\frac{6\sqrt{7}}{7}$asinBsinC,a=3,b=2,则c=2.分析 利用正弦定理化简已知,结合余弦定理,可得a2+b2-c2=$\frac{6\sqrt{7}}{7}$absinC=2abcosC,化简可求tanC,利用同角三角函数基本关系式可求cosC,由余弦定理即可解得c的值.
解答 解:∵asinA+bsinB-csinC=$\frac{6\sqrt{7}}{7}$asinBsinC,
∴a2+b2-c2=$\frac{6\sqrt{7}}{7}$absinC=2abcosC,
∴$\frac{6\sqrt{7}}{7}$sinC=2cosC,可得:tanC=$\frac{2\sqrt{7}}{6}$,cosC=$\sqrt{\frac{1}{1+ta{n}^{2}C}}$=$\frac{3}{4}$,
∵a=3,b=2,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{9+4-{c}^{2}}{2×3×2}$=$\frac{3}{4}$,
∴解得:c=2.
故答案为:2.
点评 本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
20.函数y=$\frac{2x-1}{\sqrt{3x+5}}$的定义域为( )
| A. | {x|x≥-$\frac{5}{3}$} | B. | {x|x≥-$\frac{5}{3}$且x≠$\frac{1}{2}$} | C. | {x|x>-$\frac{5}{3}$} | D. | {x|x≤-$\frac{5}{3}$} |
5.执行如图的程序框图(n∈N*),则输出的S=( )
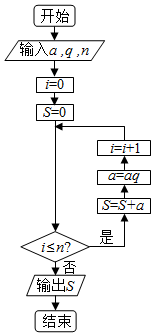

| A. | a+aq+…+aqn-1 | B. | $\frac{{a(1-{q^n})}}{1-q}$ | C. | a+aq+…+aqn | D. | $\frac{{a(1-{q^{n+1}})}}{1-q}$ |
15.执行如图所示的程序框图,若输入n=10,则输出的S=( )
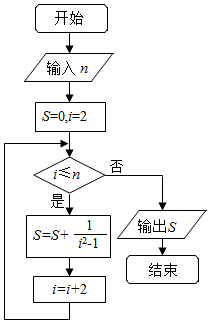

| A. | $\frac{5}{11}$ | B. | $\frac{20}{21}$ | C. | $\frac{10}{21}$ | D. | $\frac{10}{11}$ |
20.设P(x,y)满足$\left\{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y≤4}\end{array}\right.$,点A(2,0),B(0,3),若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,O是坐标原点,则λ+μ的取值范围是( )
| A. | [2,4] | B. | [$\frac{5}{6}$,$\frac{11}{6}$] | C. | [$\frac{5}{6}$,2] | D. | [1,2] |