题目内容
圆柱的轴截面是边长为10的正方形，则圆柱的侧面积为（ ）
| A、50π | B、100π |
| C、125π | D、100+25π |
考点：棱柱、棱锥、棱台的侧面积和表面积
专题：空间位置关系与距离
分析：根据圆柱的轴截面是正方形，求出圆柱的底面圆的周长，代入侧面积公式计算．
解答：
解：∵圆柱的轴截面是正方形，且边长为10，
∴圆柱的周长为：10π，
∴圆柱的侧面积S=10×10π=100π．
故选B．
∴圆柱的周长为：10π，
∴圆柱的侧面积S=10×10π=100π．
故选B．
点评：本题考查了圆柱的侧面积及轴截面，属于基础题．
练习册系列答案
相关题目
在数列{an}中，a1=1，对任意n∈N*，有an+1=
，则a10=（ ）
| an |
| 1+an |
| A、10 | ||
B、
| ||
| C、5 | ||
D、
|
已知x∈[-π，π]，则“x∈[-
，
]是“sin（sinx）＜cos（cosx）成立”的（ ）
| π |
| 2 |
| π |
| 2 |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
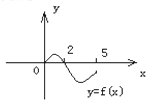若一个函数y=f（x）的图象关于y轴对称，则称这个函数为偶函数，设偶函数y=f（x）的定义域为[-5，5]，若当x∈[0，5]时，函数y=f（x）的图象如下图，则f（x）＜0解集是（ ）| A、（-2，0）∪（2，5] |
| B、（-5，-2）∪（2，5） |
| C、[-2，0]∪（2，5] |
| D、[-5，-2）∪（2，5] |
f（x）在定义域（0，+∞）上单调递增，则不等式f（x）＞f[8（x-2）]的解集是（ ）
A、（0，
| ||
B、（-∞，
| ||
C、（2，
| ||
D、（
|
下列函数中是奇函数的是（ ）
| A、y=x+x2 | ||
| B、y=|x|-2 | ||
C、y=
| ||
| D、y=-x2+1 |
如图，正六边形ABCDEF的边长为1，则
•
=（ ）
| AD |
| DB |
| A、-3 | ||
B、-
| ||
| C、3 | ||
D、
|