题目内容
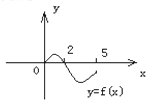 若一个函数y=f(x)的图象关于y轴对称,则称这个函数为偶函数,设偶函数y=f(x)的定义域为[-5,5],若当x∈[0,5]时,函数y=f(x)的图象如下图,则f(x)<0解集是( )
若一个函数y=f(x)的图象关于y轴对称,则称这个函数为偶函数,设偶函数y=f(x)的定义域为[-5,5],若当x∈[0,5]时,函数y=f(x)的图象如下图,则f(x)<0解集是( )| A、(-2,0)∪(2,5] |
| B、(-5,-2)∪(2,5) |
| C、[-2,0]∪(2,5] |
| D、[-5,-2)∪(2,5] |
考点:奇偶函数图象的对称性
专题:函数的性质及应用
分析:由当x∈[0,5]时,函数y=f(x)的图象,先求出当x∈[0,5]时,f(x)<0的解集,再根据函数图象的对称性,求出当x∈[-5,0]时,f(x)<0的解集,综合讨论结果,可得答案.
解答:
解:∵函数y=f(x)的图象关于y轴对称,
当x∈[0,5]时,若函数y=f(x)<0,
则x∈(2,5],
故当x∈[-5,0]时,若函数y=f(x)<0,
则x∈[-5,-2),
综上f(x)<0的解集是[-5,-2)∪(2,5],
故选:D
当x∈[0,5]时,若函数y=f(x)<0,
则x∈(2,5],
故当x∈[-5,0]时,若函数y=f(x)<0,
则x∈[-5,-2),
综上f(x)<0的解集是[-5,-2)∪(2,5],
故选:D
点评:本题考查的知识点是奇偶函数图象的对称性,难度不大,属于基础题.

练习册系列答案
相关题目
关于x的一元二次方程x2-3x+m=0有两个不相等的实数根,则实数m的取值范围为( )
A、m>
| ||
B、m=
| ||
C、m<
| ||
D、m<-
|
如果数列{an}满足a1=1,当n为奇数时,an+1=2an;当n为偶数时,an+1=an+2,则下列结论成立的是( )
| A、该数列的奇数项成等比数列,偶数项成等差数列 |
| B、该数列的奇数项成等差数列,偶数项成等比数列 |
| C、该数列的奇数项各项分别加4后构成等比数列 |
| D、该数列的偶数项各项分别加4后构成等比数列 |
下列说法正确的是( )
| A、某事件发生的频率是客观存在的,与试验次数无关 |
| B、某事件发生的概率为0,则该事件是不可能事件 |
| C、某事件发生的概率是随机的,在实验前不能确定 |
| D、每个实验结果出现的频率之和一定等于1 |
圆柱的轴截面是边长为10的正方形,则圆柱的侧面积为( )
| A、50π | B、100π |
| C、125π | D、100+25π |
把函数f(x)的图象向右平移一个单位长度,所得图象恰与函数y=ex的图象关于直线y=x对称,则f(x)=( )
| A、ln(x-1) |
| B、lnx-1 |
| C、ln(x+1) |
| D、lnx+1 |
下列关系式正确的是( )
A、
| ||
| B、{a,b}={b,a} | ||
| C、{2}={x|x2=2x} | ||
| D、∅∈{2014} |
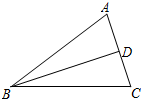 在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5,cos∠ABC=
在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5,cos∠ABC=