题目内容
设平面向量
=(4,-3),
=(2,1)若
+t
与
的夹角是
,求实数t的值( )
| a |
| b |
| a |
| b |
| b |
| π |
| 4 |
| A、-3 | B、1 |
| C、-3或1 | D、以上都不对 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由已知得
+t
与
的夹角是
,用坐标表示
+t
,得出关于t的方程,解方程即得t的值.
| a |
| b |
| b |
| π |
| 4 |
| a |
| b |
解答:
解:向量
=(4,-3),
=(2,1),
∴
+t
=(4-2t,-3-t);
又∵
+t
与
的夹角是
,
∴(
+t
)
=|
+t
||
|cos
,
即2(4-2t)+1×(-3-t)=
×
×
,
化简,得1-t=
×
,
即
,
解得t=-1;
∴t的值是-1.
故选D.
| a |
| b |
∴
| a |
| b |
又∵
| a |
| b |
| b |
| π |
| 4 |
∴(
| a |
| b |
| b |
| a |
| b |
| b |
| π |
| 4 |
即2(4-2t)+1×(-3-t)=
| (4-2t)2+(-3-t)2 |
| 5 |
| ||
| 2 |
化简,得1-t=
| t2-2t+5 |
| ||
| 2 |
即
|
解得t=-1;
∴t的值是-1.
故选D.
点评:本题考查了平面向量的应用问题,解题时应利用坐标表示写出向量的数量积,得到关于t的方程,解方程即可,是基础题.

练习册系列答案
相关题目
已知变量x,y的值如表所示;如果y与x线性相关且回归直线方程为y=bx+
,则实数b=( )
| 7 |
| 2 |
| x | 2 | 3 | 4 |
| y | 5 | 4 | 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
曲线C的方程为
+
=1,其中m,n是将一枚骰子先后投掷两次所得点数,事件A=“方程
+
=1表示焦点在x轴上的椭圆”,那么P(A)=( )
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示,在河岸 ac一侧测量河的宽度,测量以下四组数据,较适宜的是( ) 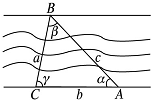

| A、c,α,γ |
| B、c,b,α |
| C、c,a,β |
| D、b,α,γ |
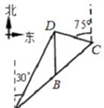 如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.
如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.