题目内容
已知函数f(x)=2sinx+2
cosx,(x∈R)
①求函数f(x)的最大值和最小值;
②求f(x)的单调递区间.
| 3 |
①求函数f(x)的最大值和最小值;
②求f(x)的单调递区间.
考点:两角和与差的正弦函数,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(1)利用两角和公式对函数解析式化简整理,利用三角函数的性质求得函数的最大和最小值.
(2)利用(1)的函数解析式,利用三角函数的性质和图象求得函数的单调增和单调减区间.
(2)利用(1)的函数解析式,利用三角函数的性质和图象求得函数的单调增和单调减区间.
解答:
解:(1)f(x)=2sinx+2
cosx=4(
sinx+
cosx)=4sin(x+
),
∵1≤sin(x+
)≤1
∴-4≤4sin(x+
)≤4
即函数f(x)的最大值为4,最小值为-4
(2)当2kπ-
≤x+
≤2kπ+
时,即2kπ-
≤x≤2kπ+
时,k∈Z,
函数单调增,
∴函数的单调增区间为[2kπ-
,2kπ+
](k∈Z),
当2kπ+
≤x+
≤2kπ+
时,即2kπ+
≤x≤2kπ+
时,k∈Z,函数单调减,
∴函数f(x)的单调减区间为[2kπ+
,2kπ+
](.k∈Z).
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∵1≤sin(x+
| π |
| 3 |
∴-4≤4sin(x+
| π |
| 3 |
即函数f(x)的最大值为4,最小值为-4
(2)当2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| π |
| 6 |
函数单调增,
∴函数的单调增区间为[2kπ-
| 5π |
| 6 |
| π |
| 6 |
当2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
∴函数f(x)的单调减区间为[2kπ+
| π |
| 6 |
| 7π |
| 6 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.在解决三角函数问题时,常与三角函数图象结合,利用数形结合的方法来解决问.

练习册系列答案
相关题目
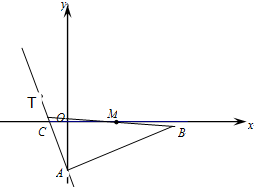 如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).
如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).