题目内容
设数列{an}满足a1=2,an+1=4an-3n+1,n∈N*,则数列{an}的前n项和为 .
考点:数列的求和
专题:等差数列与等比数列
分析:本题可根据已知条件构造新数列,由新数列的通项公式得到数列{an}的通项公式,再对数列{an}用进行分组求和的方法求和,得到本题结论.
解答:
解:∵an+1=4an-3n+1,
∴an+1-(n+1)=4(an-n),
∵a1=2,
∴a1-1=1,
∴数列{an-n}是以1为首项,公比为4的等比数列.
∴an-n=1×4n-1=4n-1.
即an=4n-1+n.
∴Sn=(1+1)+(4+2)+(42+3)++(4n-1+n)
=(1+4+42+…+4n-1)+(1+2+3+…+n)
=
+
=
+
.
故应填
+
.
∴an+1-(n+1)=4(an-n),
∵a1=2,
∴a1-1=1,
∴数列{an-n}是以1为首项,公比为4的等比数列.
∴an-n=1×4n-1=4n-1.
即an=4n-1+n.
∴Sn=(1+1)+(4+2)+(42+3)++(4n-1+n)
=(1+4+42+…+4n-1)+(1+2+3+…+n)
=
| 1(1-4n) |
| 1-4 |
| n(n+1) |
| 2 |
=
| n(n+1) |
| 2 |
| 4n-1 |
| 3 |
故应填
| n(n+1) |
| 2 |
| 4n-1 |
| 3 |
点评:本题考查了等比数列的定义、通项公式及前n项和公式,用到了构造新数列的办法求通项公式,还用了分组求和的方法求前n项的和.本题有一定的维度,属于中档题.

练习册系列答案
相关题目
已知平面向量
,
满足|
|=1,|
|=2,且(
-
)⊥
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
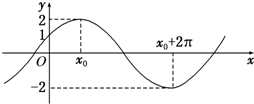 如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<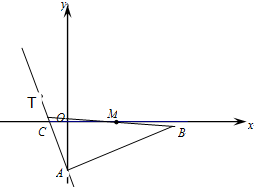 如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).
如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).