题目内容
已知函数f（x）=ex-1，g（x）=-x2+4x-3，若有f（a）=g（b），则a的取值范围为（ ）
A、[2-
| ||||
| B、（-∞，ln2] | ||||
C、（2-
| ||||
| D、（ln2，+∞） |
考点：函数的值域
专题：函数的性质及应用
分析：根据函数的单调性求出g（x）的值域，从而得到f（a）的取值范围，解一元二次不等式即可．
解答：
解：∵g（x）=-x2+4x-3，
∴g（x）≤g（2）=1，
∵f（x）=ex-1，
∴ea-1≤1，ea≤2，
即a≤ln2，
故选：B
∴g（x）≤g（2）=1，
∵f（x）=ex-1，
∴ea-1≤1，ea≤2，
即a≤ln2，
故选：B
点评：本题考查了函数的值域以及函数的定义域和一元二次不等式的解法问题，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某人午休醒来，发觉表停了，他打开收音机想收听电台整点报时，则他等待的时间短于5分钟的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知某几何本的直观图和三视图如图，则下列判定正确的是（ ）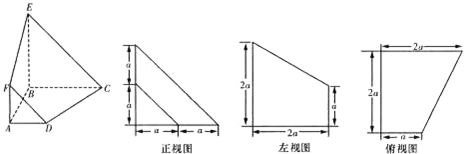
| A、DF∥CE，且BA、CD、EF的延长线不交于同一点 |
| B、DF∥CE，且BA、CD、EF的延长线交于一点 |
| C、DF与CE是异面直线 |
| D、DF与CE相交于一点 |
如图，在四棱锥P-ABCD中，PA=PB=PD=AB=BC=CD=DA=DB=2，E为的PC中点．