Question

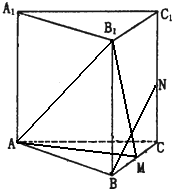如图所示，正三棱柱ABC-A₁B₁C₁中，各棱长均为4，M、N分别是BC、CC₁的中点．
（1）证明：MN⊥平面AMB；
（2）求三棱锥B₁-ABC的侧面积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面垂直的判定

专题：空间位置关系与距离

分析：（1）确定BN⊥B₁M，AM⊥BN，运用判断定理可以得出MN⊥平面AMB；
（2）计算△B₁BA，△B₁BC，△B₁AC的面积，可得出侧面积．

解答： 证明：（1）∵正三棱柱ABC-A₁B₁C₁中，各棱长均为4，M、N分别是BC、CC₁的中点．
∴BN⊥B₁M，
∵AM⊥面BB₁C₁C，BN?面BB₁C₁C
∴AM⊥BN，
∵AM∩B₁M=M，
∴MN⊥平面AMB；
解：（2设）△B₁BA，△B₁BC，△B₁AC的面积为：S₁，S₂，S₃，
∵S₁=

1

2

×4×4=8，S₂=

1

2

×4×4=8，S₃=

1

2

×4×

(4 2 )2-22

=4

7

，
∴三棱锥B₁-ABC的侧面积=

1

2

×4×4+

1

2

×4×4+

1

2

×4×2

7

=16+4

7

，

点评：本题考查了空间直线，平面的垂直问题，计算面积问题，难度不大，注意计算准确即可．