题目内容
已知函数f(x)=(sinx+cosx)2+
(2cos2x-1),x∈R.
(Ⅰ)若对任意x恒有f(-
)≤f(ωx+φ)≤f(
),(ω>0,|φ|<
),求ω的最小值和对应的φ的值.
(Ⅱ)若△ABC的角A、B、C所对的边分别是a,b,c,且f(
)=1,又b,a,4c成等比数列,求
的值.
| 3 |
(Ⅰ)若对任意x恒有f(-
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
(Ⅱ)若△ABC的角A、B、C所对的边分别是a,b,c,且f(
| A |
| 2 |
| sinB |
| sinC |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)首先,化简函数解析式,得到f(x)=2sin(2x+
)+1,然后,依据f(-
)≤f(ωx+φ)≤f(
)恒成立,得到
T的最大值为:
-(-
)=
,从而求解即可;
(Ⅱ)根据f(
)=1,得到A=
,然后,结合边的关系和正弦定理,求解其比值即可.
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
(Ⅱ)根据f(
| A |
| 2 |
| 2π |
| 3 |
解答:
解:(Ⅰ)f(x)=(sinx+cosx)2+
(2cos2x-1)
=1+sin2x+
cos2x
=2sin(2x+
)+1,
∴f(ωx+φ)=2sin(2ωx+2φ+
)+1,设其最小正周期为T,
由题意知,
Tmax=
-(-
)=
,
∴Tmax=π,
∴ωmin=1,
同时,2×
+2φ+
=
+2kπ,k∈z,
又∵|Φ|<
,
∴φ=
.
(Ⅱ)∵f(
)=1,
∴2sin(A+
)+1=1,
∴sin(A+
)=0,
∵A∈(0,π)
∴A=
,
∵b,a,4c成等比数列,
∴a2=4bc,
由余弦定理,得
a2=b2+c2-2bccosA,得
∴b2+c2-bc=4bc,
∴(
)2-3
+1=0,
∴
=
,
根据正弦定理,得
=
,
∴
=
,
∴
的值
.
| 3 |
=1+sin2x+
| 3 |
=2sin(2x+
| π |
| 3 |
∴f(ωx+φ)=2sin(2ωx+2φ+
| π |
| 3 |
由题意知,
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴Tmax=π,
∴ωmin=1,
同时,2×
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
又∵|Φ|<
| π |
| 2 |
∴φ=
| π |
| 4 |
(Ⅱ)∵f(
| A |
| 2 |
∴2sin(A+
| π |
| 3 |
∴sin(A+
| π |
| 3 |
∵A∈(0,π)
∴A=
| 2π |
| 3 |
∵b,a,4c成等比数列,
∴a2=4bc,
由余弦定理,得
a2=b2+c2-2bccosA,得
∴b2+c2-bc=4bc,
∴(
| b |
| c |
| b |
| c |
∴
| b |
| c |
3±
| ||
| 2 |
根据正弦定理,得
| b |
| sinB |
| c |
| sinC |
∴
| sinB |
| sinC |
| b |
| c |
∴
| sinB |
| sinC |
3±
| ||
| 2 |
点评:本题重点考查了余弦定理、正弦定理、三角恒等变换公式等知识,属于中档题.

练习册系列答案
相关题目
已知某几何本的直观图和三视图如图,则下列判定正确的是( )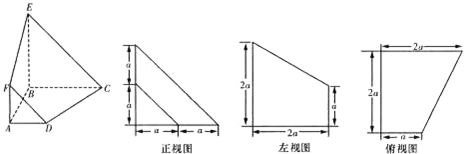

| A、DF∥CE,且BA、CD、EF的延长线不交于同一点 |
| B、DF∥CE,且BA、CD、EF的延长线交于一点 |
| C、DF与CE是异面直线 |
| D、DF与CE相交于一点 |
如图所示的程序框图运行的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|