题目内容
证明:(1)对于任意n≥3,n∈N*,
+
+
+…+
>
;
(2)对于任意n≥2,n∈N*,
+
+
+…+
<2-
.
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| n+1 |
(2)对于任意n≥2,n∈N*,
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| n |
考点:不等式的证明
专题:证明题
分析:(1)利用
>
=2(
-
),累加所证不等式的左端,即可证得原不等式成立;
(2)利用当n≥2时,
<
=
-
,累加所证不等式的左端,即可证得原不等式成立.
| 1 | ||
|
| 2 | ||||
|
| n+1 |
| n |
(2)利用当n≥2时,
| 1 |
| n2 |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
解答:
证明:(1)∵
=
>
=2(
-
),
∴
+
+
+…+
>
+
+2[(
-
)+(
-
)+…+(
-
)]
=
+
+2(
-
)=
+(1+
+
-
),
∵n≥3,n∈N*,
∴1+
+
-
>0,
∴对于任意n≥3,n∈N*,
+
+
+…+
>
;
(2)∵当n≥2时,
<
=
-
,
∴
+
+
+…+
<
+[(1-
)+(
-
)+…+(
-
)]
=1+(1-
)=2-
,
即对于任意n≥2,n∈N*,
+
+
+…+
<2-
.
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
| n+1 |
| n |
∴
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 4 |
| 3 |
| 5 |
| 4 |
| n+1 |
| n |
=
| 1 | ||
|
| 1 | ||
|
| n+1 |
| 3 |
| n+1 |
| ||
| 2 |
| n+1 |
| 3 |
∵n≥3,n∈N*,
∴1+
| ||
| 2 |
| n+1 |
| 3 |
∴对于任意n≥3,n∈N*,
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| n+1 |
(2)∵当n≥2时,
| 1 |
| n2 |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
=1+(1-
| 1 |
| n |
| 1 |
| n |
即对于任意n≥2,n∈N*,
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| n |
点评:本题考查不等式的证明,着重考查放缩法与裂项法的综合应用,考查推理论证能力,属于中档题.

练习册系列答案
相关题目
已知
,
为互相垂直的单位向量,若向量λ
+
与
+λ
的夹角等于30°,则实数λ等于( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
A、±2
| ||||||
B、±
| ||||||
C、±
| ||||||
D、
|
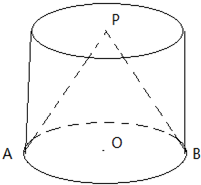 已知一个圆柱和一个圆锥等底等高,如图,点O为底面的圆心,点P为圆锥的顶点.若圆柱的高等于它的底面直径.
已知一个圆柱和一个圆锥等底等高,如图,点O为底面的圆心,点P为圆锥的顶点.若圆柱的高等于它的底面直径.