Question

在x轴的正方向上，从左向右依次取点列{A_j}，j=1，2…，以及在第一象限内的抛物线y²=

3

2

x上从左向右依次取点列{B_k}，k=1，2…，使△A_k-1B_kA_k（k=1，2…）都是等边三角形，其中A₀是坐标原点，则第2005个等边三角形的边长是

 

．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：利用等边三角形的性质可得：直线A₀B₁的斜率及其方程，与抛物线方程联立可得点B₁的坐标，即可得出第一个等边三角形的边长，依此类推即可得出第2005个等边三角形的边长．

解答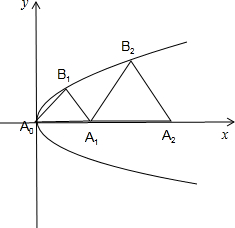： 解：如图所示，
∵△A₀B₁A₁是等边三角形，
∴∠B₁A₀A₁=60°．
∴直线A₀B₁的方程为；y=

3

x．
联立

y= 3 x y2= 3 2 x

，解得

x= 1 2 y= 3 2

，
可得第一个等边三角形的边长=1．
同理联立

y= 3 (x-1) y2= 3 2 x

，解得x=2，
可得第二个等边三角形的边长=2×（2-1）=2．
…，
可得第2005个等边三角形的边长是2005．
故答案为：2005．

点评：本题考查了等边三角形的性质、直线与抛物线相交问题转化为方程联立、类比推理等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．