题目内容
函数y=Asin(ωx+φ)(A>0,ω>0,0≤φ≤
)在x∈(0,7π)内只取到一个最大值和一个最小值,且当x=π时,ymax=3;当x=6π时,ymin=-3.
(1)求此函数的解析式;
(2)求此函数的单调递增区间.
| π |
| 2 |
(1)求此函数的解析式;
(2)求此函数的单调递增区间.
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)由函数的最值求出A,由周期求出ω,由图象经过定点求出φ的值,从而求得函数的解析式.
(2)令2kπ-
≤
x+
≤2kπ+
,k∈z,求得x的范围,可得函数的增区间.
(2)令2kπ-
| π |
| 2 |
| 1 |
| 5 |
| 3π |
| 10 |
| π |
| 2 |
解答:
解:(1)由题意可得,A=3,周期T=2(6π-π)=10π=
,∴ω=
.
再根据点(π,3)在函数的图象上,可得3sin(
π+φ)=3,可得sin(
+φ)=1.
结合0≤φ≤
,可得φ=
,∴函数的解析式为y=3sin(
x+
).
(2)令2kπ-
≤
x+
≤2kπ+
,k∈z,求得10kπ-4π≤x≤10kπ+π,k∈z,
故函数的增区间为[10kπ-4π,10kπ+π],k∈z.
| 2π |
| ω |
| 1 |
| 5 |
再根据点(π,3)在函数的图象上,可得3sin(
| 1 |
| 5 |
| π |
| 5 |
结合0≤φ≤
| π |
| 2 |
| 3π |
| 10 |
| 1 |
| 5 |
| 3π |
| 10 |
(2)令2kπ-
| π |
| 2 |
| 1 |
| 5 |
| 3π |
| 10 |
| π |
| 2 |
故函数的增区间为[10kπ-4π,10kπ+π],k∈z.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的增区间,属于中档题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
设奇函数f(x)=cos(ωx+φ)-
sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,则ω,φ分别是( )
| 3 |
| π |
| 2 |
A、2,
| ||||
B、
| ||||
C、
| ||||
D、2,
|
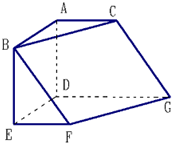 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2. 已知函数f(x)=3sin(2x-
已知函数f(x)=3sin(2x-