题目内容
设数列{an}的前n项和为Sn,且满足3Sn=4028+an(n∈N*).
(1)求数列{an}的通项公式;
(2)设f(n)表示该数列的前n项的乘积,问n取何值时,f(n)有最大值?
(1)求数列{an}的通项公式;
(2)设f(n)表示该数列的前n项的乘积,问n取何值时,f(n)有最大值?
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)在数列递推式中,取n=1求出首项,当n≥2时取n=n-1得另一递推式,作出得到数列{an}为等比数列,然后由等比数列的通项公式得答案;
(2)由通项公式可得,n≤11时,|an|>1,n≥12时,|an|<1,由此得到|f(n)|的增减性,再结合对应函数值的符号可知f(9)或f(12)最大,作比可得当n=12时,f(n)有最大值.
(2)由通项公式可得,n≤11时,|an|>1,n≥12时,|an|<1,由此得到|f(n)|的增减性,再结合对应函数值的符号可知f(9)或f(12)最大,作比可得当n=12时,f(n)有最大值.
解答:
解:(1)由3Sn=4028+an(n∈N*) ①
当n=1时,3a1=4028+a1,
得a1=2014;
当n≥2时,有3sn-1=4028+an-1 ②
①-②得:3an=an-an-1,即an=-
an-1(n≥2).
∴数列{an}是以2014为首项,-
为公比的等比数列.
∴an=2014(-
)n-1;
(2)n≤11时,|an|>1,n≥12时,|an|<1,
∴|f(n)|在n≥11时递减,在n≤11时递增,
∴|f(11)|为最大值,f(11)<0,f(10)<0,f(9)>0,f(12)>0
∵
=a10a11a12>1,
∴当n=12时,f(n)有最大值.
当n=1时,3a1=4028+a1,
得a1=2014;
当n≥2时,有3sn-1=4028+an-1 ②
①-②得:3an=an-an-1,即an=-
| 1 |
| 2 |
∴数列{an}是以2014为首项,-
| 1 |
| 2 |
∴an=2014(-
| 1 |
| 2 |
(2)n≤11时,|an|>1,n≥12时,|an|<1,
∴|f(n)|在n≥11时递减,在n≤11时递增,
∴|f(11)|为最大值,f(11)<0,f(10)<0,f(9)>0,f(12)>0
∵
| f(12) |
| f(9) |
∴当n=12时,f(n)有最大值.
点评:本题考查数列递推式,考查了数列通项公式的求法,考查了数列的函数特性,是中档题.

练习册系列答案
相关题目
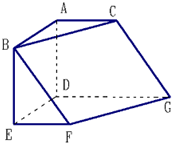 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.