题目内容
水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为:V(t)=
.
(1)该水库的蓄水量小于50的时期称为枯水期,以t表示第t月份(t=1,2,3,…,12),问:同一年内哪些月份是枯水期?
(2)求一年内哪个月份该水库的蓄水量最大,并求最大蓄水量.
|
(1)该水库的蓄水量小于50的时期称为枯水期,以t表示第t月份(t=1,2,3,…,12),问:同一年内哪些月份是枯水期?
(2)求一年内哪个月份该水库的蓄水量最大,并求最大蓄水量.
考点:导数在最大值、最小值问题中的应用,函数模型的选择与应用
专题:应用题,函数的性质及应用,导数的综合应用
分析:(1)分段求出水库的蓄求量小于50时x的取值范围,注意实际问题x要取整.
(2)一年内该水库的最大蓄水量肯定不在枯水期,则V(t)的最大值只能在(4,10)内达到,然后通过导数在给定区间上研究V(t)的最大值.
(2)一年内该水库的最大蓄水量肯定不在枯水期,则V(t)的最大值只能在(4,10)内达到,然后通过导数在给定区间上研究V(t)的最大值.
解答:
解:(1)当0<t≤10时,V(t)=(-t2+14t-40)e
t+50<50,化简得t2-14t+40>0,
∴t<4或t>10,又0<t≤10,故0<t<4.----------------------------------------------------2分
当10<t≤12时,V(t)=4(t-10)(3t-41)+50<50,化简得(t-10)(3t-41)<0
∴10<t<
,又10<t≤12,故10<t≤12------------------------------------------------4分
综上得,0<t<4或10<t≤12-------------------------------------------------------------5分
故知枯水期为1月、2月、3月、11月、12月共5个月.---------------------------7分
(2)由(1)可知V(t)的最大值只能在[4,10]内达到.--------------------------------8分
由V′(t)=e
(-
t2+
+4)=-
e
(t+2)(t-8)------------------------------------9分
令V'(t)=0得t=8或t=-2(舍去)------------------------------------------------------10分
当t变化时,V'(t)与V(t)的变化情况如下表
------12分
由上表可知,V(t)在t=8时取得最大值8e2+50(亿立方米).------------------13分
故知一年内该水库的最大蓄水量是8e2+50亿立方米.--------------------------------14分.
| 1 |
| 4 |
∴t<4或t>10,又0<t≤10,故0<t<4.----------------------------------------------------2分
当10<t≤12时,V(t)=4(t-10)(3t-41)+50<50,化简得(t-10)(3t-41)<0
∴10<t<
| 41 |
| 3 |
综上得,0<t<4或10<t≤12-------------------------------------------------------------5分
故知枯水期为1月、2月、3月、11月、12月共5个月.---------------------------7分
(2)由(1)可知V(t)的最大值只能在[4,10]内达到.--------------------------------8分
由V′(t)=e
| t |
| 4 |
| 1 |
| 4 |
| 3t |
| 2 |
| 1 |
| 4 |
| t |
| 4 |
令V'(t)=0得t=8或t=-2(舍去)------------------------------------------------------10分
当t变化时,V'(t)与V(t)的变化情况如下表
| t | [4,8) | 8 | (8,10] |
| V'(t) | + | 0 | - |
| V(t) | ↑ | 8e2+50 | ↓ |
由上表可知,V(t)在t=8时取得最大值8e2+50(亿立方米).------------------13分
故知一年内该水库的最大蓄水量是8e2+50亿立方米.--------------------------------14分.
点评:本小题主要考查函数、导数和不等式等基本知识,考查用导数求最值和综合运用数学知识解决实际问题能力.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知命题p:函数y=
的定义域是(-∞,-3]∪[1,+∞);命题q:若a,b∈R,则|a+b|<1是|a|+|b|<1的充分而不必要条件,则下列命题中为真命题的是( )
| |x+1|-2 |
| A、p∧q |
| B、(¬p)∨q |
| C、p∨(¬q) |
| D、(¬p)∧(¬q) |
 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.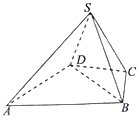 已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB,
已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB,