题目内容
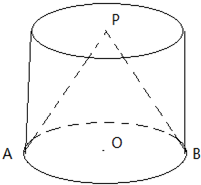 已知一个圆柱和一个圆锥等底等高,如图,点O为底面的圆心,点P为圆锥的顶点.若圆柱的高等于它的底面直径.
已知一个圆柱和一个圆锥等底等高,如图,点O为底面的圆心,点P为圆锥的顶点.若圆柱的高等于它的底面直径.(1)求证:圆柱的任意一条母线和圆锥的任意一条母线所成的角都相等;
(2)求圆柱的全面积和圆锥的全面积的比值.
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:设圆柱的高为h,底面半径为r,圆锥的母线长为l,h=2r,
(1)通过圆锥的任意一条母线与轴OP组成全等的直角三角形,证明即可.
(2)求出圆柱的全面积和圆锥的全面积,即可得到它们的比值.
(1)通过圆锥的任意一条母线与轴OP组成全等的直角三角形,证明即可.
(2)求出圆柱的全面积和圆锥的全面积,即可得到它们的比值.
解答:
 解:设圆柱的高为h,底面半径为r,圆锥的母线长为l,h=2r.
解:设圆柱的高为h,底面半径为r,圆锥的母线长为l,h=2r.
(1)因为圆柱的所有母线都平行于OP,圆锥的任意一条母线与轴OP组成全等的直角三角形,
如图,∠APO为圆柱的母线和圆锥的母线所成的角.…(2分).
在Rt△AOP中,tan∠APO=
=
,则∠APO=arctan
…(4分)
∴,圆柱的任意一条母线和圆锥的任意一条母线所成的角都相等,为arctan
.…(6分)
(2)h=2r,l=
=
r…(8分)
S柱=2πrh+2πr2=6πr2,…(9分)
S锥=πr2+
l•2πr=(1+
)πr…(10分)
故
=
=
(
-1).…(12分)
 解:设圆柱的高为h,底面半径为r,圆锥的母线长为l,h=2r.
解:设圆柱的高为h,底面半径为r,圆锥的母线长为l,h=2r.(1)因为圆柱的所有母线都平行于OP,圆锥的任意一条母线与轴OP组成全等的直角三角形,
如图,∠APO为圆柱的母线和圆锥的母线所成的角.…(2分).
在Rt△AOP中,tan∠APO=
| OA |
| AP |
| 1 |
| 2 |
| 1 |
| 2 |
∴,圆柱的任意一条母线和圆锥的任意一条母线所成的角都相等,为arctan
| 1 |
| 2 |
(2)h=2r,l=
| h2+r2 |
| 5 |
S柱=2πrh+2πr2=6πr2,…(9分)
S锥=πr2+
| 1 |
| 2 |
| 5 |
故
| S柱 |
| S锥 |
| 6 | ||
1+
|
| 3 |
| 2 |
| 5 |
点评:本题考查旋转体的表面积与体积的求法,考查计算能力.

练习册系列答案
相关题目
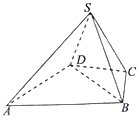 已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB,
已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB, 已知函数f(x)=3sin(2x-
已知函数f(x)=3sin(2x- 如图是甲、乙两名同学三次测验成绩的茎叶图,则甲、乙两名同学中成绩更稳定的是
如图是甲、乙两名同学三次测验成绩的茎叶图,则甲、乙两名同学中成绩更稳定的是