题目内容
函数f(x)=
+lg(3x+1)的定义域为( )
| x2+4 | ||
|
A、(-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:要使函数的解析式有意义,自变量x须满足被开方数≥0且对数的真数>0,同时分母不为0,解不等式后,可得答案.
解答:
解:要使函数的解析式有意义
自变量x须满足:
,
解得-
<x<1
故函数f(x)的定义域为(-
,1)
故选:C
自变量x须满足:
|
解得-
| 1 |
| 3 |
故函数f(x)的定义域为(-
| 1 |
| 3 |
故选:C
点评:本题考查的知识点是函数的定义域及其求法,其中根据使函数的解析式有意义的原则,构造不等式是解答的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
双曲线
-x2=1的渐近线方程为( )
| y2 |
| 3 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
设集合M={y|y=|sinx|,x∈R},N={x||x|<1},则M∩N=( )
| A、(0,1) |
| B、(0,1] |
| C、[0,1) |
| D、[0,1] |
在平行四边形ABCD中,AC与BD交于点M,则
+
=( )
| AB |
| CM |
A、
| ||
B、
| ||
C、
| ||
D、
|
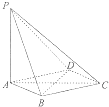 如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.