题目内容
给出下列命题:
(1)函数f(x)=2xln(x-2)-3只有一个零点;
(2)若
与
不共线,则
+
与
-
不共线;
(3)若非零平面向量
,
,
两两所成的夹角均相等,则夹角为120°;
(4)若数列{an}的前n项的和Sn=2n+1-1,则数列{an}是等比数列;
(5)函数y=2x的图象经过一定的平移可以得到函数y=3•2x-1的图象.
其中,所有正确命题的序号为 .
(1)函数f(x)=2xln(x-2)-3只有一个零点;
(2)若
| a |
| b |
| a |
| b |
| a |
| b |
(3)若非零平面向量
| a |
| b |
| c |
(4)若数列{an}的前n项的和Sn=2n+1-1,则数列{an}是等比数列;
(5)函数y=2x的图象经过一定的平移可以得到函数y=3•2x-1的图象.
其中,所有正确命题的序号为
考点:命题的真假判断与应用
专题:函数的性质及应用,等差数列与等比数列,平面向量及应用,简易逻辑
分析:(1)根据函数y=ln(x-2)和函数y=
的图象有且只有一个交点,可得函数f(x)=2xln(x-2)-3只有一个零点;
(2)利用反证法,结合向量共线的充要条件,可判断正误;
(3)若非零平面向量
,
,
两两所成的夹角均相等,则夹角为120°或0°;
(4)若数列{an}的前n项的和Sn=2n+1-1,可求出数列的前若干项,进而可判断正误;
(5)函数y=3•2x-1=2x+log23-1,根据函数图象的平移变换法则,可判断正误.
| ||
| x |
(2)利用反证法,结合向量共线的充要条件,可判断正误;
(3)若非零平面向量
| a |
| b |
| c |
(4)若数列{an}的前n项的和Sn=2n+1-1,可求出数列的前若干项,进而可判断正误;
(5)函数y=3•2x-1=2x+log23-1,根据函数图象的平移变换法则,可判断正误.
解答:
解:(1)函数f(x)=2xln(x-2)-3的零点个数即方程ln(x-2)=
的根的个数,即为函数y=ln(x-2)和函数y=
的图象交点个数,两个函数图象有且只有一个交点,故(1)正确;
(2)假设
+
与
-
共线,则存在实数λ,使
+
=λ(
-
),
若λ=1,则
=
,此时
与
共线,
若λ≠1,则,此时
=
,此时
与
共线,
这与
与
不共线矛盾,故假设不成立,故(2)正确;
(3)若非零平面向量
,
,
两两所成的夹角均相等,则夹角为120°或0°,故(3)错误;
(4)若数列{an}的前n项的和Sn=2n+1-1,a1=3,a2=4,a3=8,则数列{an}不是等比数列,故(4)错误;
(5)函数y=2x的图象向左平移log23个单位,再向下平移一个单位,可以得到函数y=2x+log23-1=3•2x-1的图象,故(5)正确.
故答案为:(1)(2)(5)
| ||
| x |
| ||
| x |
(2)假设
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
若λ=1,则
| b |
| 0 |
| a |
| b |
若λ≠1,则,此时
| a |
| λ+1 |
| λ-1 |
| b |
| a |
| b |
这与
| a |
| b |
(3)若非零平面向量
| a |
| b |
| c |
(4)若数列{an}的前n项的和Sn=2n+1-1,a1=3,a2=4,a3=8,则数列{an}不是等比数列,故(4)错误;
(5)函数y=2x的图象向左平移log23个单位,再向下平移一个单位,可以得到函数y=2x+log23-1=3•2x-1的图象,故(5)正确.
故答案为:(1)(2)(5)
点评:本题以命题的真假判断为载体,考查了函数的零点,向量的共线,向量的夹角,等比数列的判定,函数图象的变换等知识点,难度中档.

练习册系列答案
相关题目
双曲线
-x2=1的渐近线方程为( )
| y2 |
| 3 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
已知函数f(x)=
,若关于x的方程f(x)=k有3个不同的实根,则实数k的取值范围为( )
|
| A、[1,+∞) |
| B、(0,+∞) |
| C、(0,2) |
| D、(1,2] |
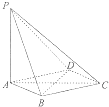 如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.