题目内容
设集合M={x|0≤x≤2},N={x|0≤y≤2},给出下四个图形,其中能构成从集合M到集合N的函数关系的是( )
A、 |
B、 |
C、 |
D、 |
考点:函数的概念及其构成要素
专题:函数的性质及应用
分析:根据函数的概念,对四个图形逐一判断即可得到答案.
解答:
解:函数的概念是给出两个非空的数集,再给出一个对应关系f,在对应关系的作用下,前一个数集中的任意一个数,在后一个数集中都有唯一确定的数和它对应,把这样的对应叫做函数,由此分析,
图①中当x∈(1,2]时,在数集N中无对应元素,故①不是;
图②中的集合M=[-1,2],所以②不是从集合M到集合N的函数;
图③中的一个x值对应了两个y值,违背函数概念,所以③不是从集合M到集合N的函数;
只有图④符合函数的图象表示.
故选;D.
图①中当x∈(1,2]时,在数集N中无对应元素,故①不是;
图②中的集合M=[-1,2],所以②不是从集合M到集合N的函数;
图③中的一个x值对应了两个y值,违背函数概念,所以③不是从集合M到集合N的函数;
只有图④符合函数的图象表示.
故选;D.
点评:本题考查了函数的图象与图象变化,解答此题的关键是理解函数实质是对应,即一对一和多对一,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
,若关于x的方程f(x)=k有3个不同的实根,则实数k的取值范围为( )
|
| A、[1,+∞) |
| B、(0,+∞) |
| C、(0,2) |
| D、(1,2] |
已知向量
=(2sinA,cosA),
=(cosA,2
cosA),
•
=
,若A∈[0,
],则A=( )
| a |
| b |
| 3 |
| a |
| b |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在平行四边形ABCD中,AC与BD交于点M,则
+
=( )
| AB |
| CM |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图,正六边形ABCDEF中,
+
+
=( )
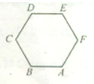
| BA |
| CD |
| BC |

A、
| ||
B、
| ||
C、
| ||
D、
|
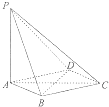 如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.