题目内容
①(极坐标与参数方程选做题)已知曲线C的极坐标方程是ρ=4cosθ.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
(t为参数),则直线l与曲线C相交所成的弦的弦长为 ;
②(不等式选做题)对于实数x,y,若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为 .
|
②(不等式选做题)对于实数x,y,若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为
考点:参数方程化成普通方程
专题:坐标系和参数方程,不等式
分析:本题①先利用公式将曲线C的极坐标方程化成直角坐标方程,再消去参数t,将直线l的参数方程化成普通方程,然后研究直线l与曲线C相交所成的弦的弦长,得到本题结论;②先将|x-2y+1|配凑成x-1,y-2的和(差)的形式,再利用绝对值不等式,求出|x-2y+1|的最大值,得到本题结论.
解答:
解:①∵
,
∴曲线C的极坐标方程是ρ=4cosθ可转化为:
ρ2=4ρcosθ,
∴x2+y2-4x=0,
∴(x-2)2+y2=4.
圆心c(2,0),半径r=2.
∵直线l的参数方程是:
(t为参数),
∴消去参数t得到:x-y-1=0.
∴圆心C(2,0)直线l的距离为:
d=
=
,
∴直线l与曲线C相交所成的弦的弦长为:
2
=
.
②∵|x-1|≤1,|y-2|≤1,
∴|x-2y+1|=|(x-1)-2(y-2)-2|≤|(x-1)|+|2(y-2)|+|2|≤1+1×2+2=5.
故答案为:(1)
;(2)5.
|
∴曲线C的极坐标方程是ρ=4cosθ可转化为:
ρ2=4ρcosθ,
∴x2+y2-4x=0,
∴(x-2)2+y2=4.
圆心c(2,0),半径r=2.
∵直线l的参数方程是:
|
∴消去参数t得到:x-y-1=0.
∴圆心C(2,0)直线l的距离为:
d=
| |2-0-1|| | ||
|
| ||
| 2 |
∴直线l与曲线C相交所成的弦的弦长为:
2
4-(
|
| 14 |
②∵|x-1|≤1,|y-2|≤1,
∴|x-2y+1|=|(x-1)-2(y-2)-2|≤|(x-1)|+|2(y-2)|+|2|≤1+1×2+2=5.
故答案为:(1)
| 14 |
点评:本题考查了参数方程与普通方程的互化、考查了绝对值不等式,本题难度不大,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知直线y=k(x+1)与抛物线C:y2=4x相交于A、B两点,F为抛物线C的焦点,若|FA|=2|FB|,则k=( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、
|
已知函数f(x)=
,若关于x的方程f(x)=k有3个不同的实根,则实数k的取值范围为( )
|
| A、[1,+∞) |
| B、(0,+∞) |
| C、(0,2) |
| D、(1,2] |
已知向量
=(2sinA,cosA),
=(cosA,2
cosA),
•
=
,若A∈[0,
],则A=( )
| a |
| b |
| 3 |
| a |
| b |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|

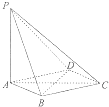 如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.