题目内容
为了对某课题进行研究,用分层抽样方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人);若从高校B、C抽取的人中选2人作专题发言,则这二人都来自高校C的概率为( )
| 高校 | 相关人数 | 抽取人数 |
| A | 18 | x |
| B | 36 | 2 |
| C | 54 | y |
| A、0.3 | B、0.4 |
| C、0.5 | D、0.6 |
考点:古典概型及其概率计算公式
专题:概率与统计,排列组合
分析:根据分层抽样方法求解得出x=1,y=3,再运用古典概率求解得出答案.
解答:
解:根据分层抽样方法得出:
=
=
,
x=1,y=3,
∴若从高校B、C抽取的人中选2人作专题发言,则这二人都来自高校C的概率为:
P(A)=
=
,
故选:A.
| 2 |
| 36 |
| x |
| 18 |
| y |
| 54 |
x=1,y=3,
∴若从高校B、C抽取的人中选2人作专题发言,则这二人都来自高校C的概率为:
P(A)=
| ||
|
| 3 |
| 10 |
故选:A.
点评:本题考查了分层抽样,古典概率的求解,属于容易题.

练习册系列答案
相关题目
某种商品若每个售价60元,则可卖出50个;已知单价每提高10元,则少卖5个,要得到最大的售货金额,售价应定为( )
| A、80元 | B、85元 |
| C、90元 | D、100元 |
已知函数f(x)=
,若k>0时,方程f(x)=k有且仅有两个不同的实数解x1、x2(x1<x2),则( )
| |sinx| |
| x |
| A、sinx1=-x1•cosx2 |
| B、sinx1=x1•cosx2 |
| C、cosx2=-x2•sinx1 |
| D、cosx2=x2•sinx1 |
下列函数中为偶函数的是( )
| A、y=3x |
| B、y=log3x |
| C、y=x2+tanx |
| D、y=1+cosx |
已知全集为U,集合A、B均为U的子集,则A∩∁UB=∅是A∪B=B的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“a<2”是“a2-2a<0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
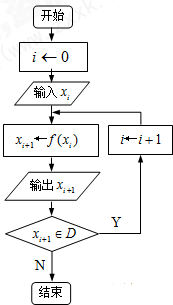 对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.