题目内容
已知函数y=
的定义域是A,函数g(x)=2(x-1)(x+3)(x∈定义域B)的值域是(1,+∞).求集合A∩B.
log
|
考点:交集及其运算
专题:集合
分析:根据根式和对数函数有意义的条件列出不等式组,求出集合A,然后根据指数函数的值域求出集合B,最后由交集的定义求出结果即可.
解答:
解:由
∴A=(1,2)
∵2(x-1)(x+3)>1
∴(x-1)(x+3)>0
∴x>1或x<-3
∴B=(1,+∞)∪(-∞,-3),
∴A∩B=A=(1,2).
|
∴A=(1,2)
∵2(x-1)(x+3)>1
∴(x-1)(x+3)>0
∴x>1或x<-3
∴B=(1,+∞)∪(-∞,-3),
∴A∩B=A=(1,2).
点评:本题属于以函数的定义域,值域的求解为平台,进而求集合的交集、补集、并集的运算的基础题,也是高考常会考的基础的题型.

练习册系列答案
相关题目
设方程sin4x=0的解集为M,方程cos2x=1的解集为P,则M与P之间的关系是( )
| A、P?M | B、M?P |
| C、M=P | D、M∩P=∅ |
如图,A地在高压线l(不计高度)的东侧0.50km处,B地在A地东北方向1.00km处,公路沿线PQ上任意一点到A地与高压线l的距离相等.现要在公路旁建一配电房向A、B两地降压供电(分别向两地进线).经协商,架设低压线路部分的费用由A、B两地用户分摊,为了使分摊费用总和最小,配电房应距高压线l( )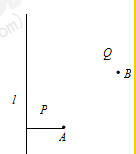
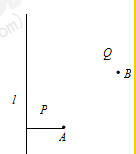
| A、1.21km |
| B、0.50km |
| C、0.75km |
| D、0.96km |
函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A)有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t度低调函数.已知定义域为[0,+∞)的函数f(x)=-|mx-3|,且f(x)为[0,+∞)上的6度低调函数,那么实数m的取值范围是( )
| A、[0,1] |
| B、[1,+∞) |
| C、(-∞,0) |
| D、(-∞,0]∪[1,+∞) |