题目内容
如图，A地在高压线l（不计高度）的东侧0.50km处，B地在A地东北方向1.00km处，公路沿线PQ上任意一点到A地与高压线l的距离相等．现要在公路旁建一配电房向A、B两地降压供电（分别向两地进线）．经协商，架设低压线路部分的费用由A、B两地用户分摊，为了使分摊费用总和最小，配电房应距高压线l（ ）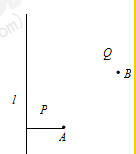
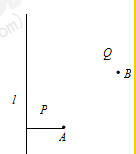
| A、1.21km |
| B、0.50km |
| C、0.75km |
| D、0.96km |
考点：函数的最值及其几何意义
专题：应用题,圆锥曲线的定义、性质与方程
分析：依题意知曲线PQ是以A为焦点、l为准线的抛物线，配电房为M，欲求分摊费用总和最小，即求抛物线上的点到A，B的距离和最小，此时BM⊥l．
解答：
解：依题意知曲线PQ是以A为焦点、l为准线的抛物线，配电房为M
建立如图所示的坐标系，则抛物线的方程为y2=x，
根据抛物线的定义知：欲求分摊费用总和最小，即求抛物线上的点到A，B的距离和最小，此时BM⊥l．
∵B地在A地东北方向1.00km处，
∴B的纵坐标为
，
∴BM⊥l时，M的坐标为（
，
），
∴配电房应距高压线l：0.5+0.25=0.75km．
故选：C．
解：依题意知曲线PQ是以A为焦点、l为准线的抛物线，配电房为M建立如图所示的坐标系，则抛物线的方程为y2=x，
根据抛物线的定义知：欲求分摊费用总和最小，即求抛物线上的点到A，B的距离和最小，此时BM⊥l．
∵B地在A地东北方向1.00km处，
∴B的纵坐标为
| ||
| 2 |
∴BM⊥l时，M的坐标为（
| 1 |
| 2 |
| ||
| 2 |
∴配电房应距高压线l：0.5+0.25=0.75km．
故选：C．
点评：本题考查了抛物线方程的应用，考查了学生根据实际问题选择函数模型的能力，考查了计算能力，是中档题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目