题目内容
设|x|≤
,求函数f(x)=cos(2x+
)的值域.
| π |
| 4 |
| π |
| 4 |
考点:三角函数的最值
专题:三角函数的图像与性质
分析:由|x|≤
,求得2x+
的范围,判定y=cos(2x+
)的增递性,求出y的最值,即得函数的值域.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:
解:∵|x|≤
,∴x∈[-
,
],
∴2x∈[-
,
],
∴2x+
∈[-
,
],
∴y=cos(2x+
)先递增,再递减;
当2x+
=0,即x=-
时,y取得最大值1,
当2x+
=
,即x=
时,y有最小值:y=-
,
∴函数的值域是[-
,1].
故答案为:[-
,1].
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∴2x∈[-
| π |
| 2 |
| π |
| 2 |
∴2x+
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴y=cos(2x+
| π |
| 4 |
当2x+
| π |
| 4 |
| π |
| 8 |
当2x+
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴函数的值域是[-
| ||
| 2 |
故答案为:[-
| ||
| 2 |
点评:本题考查了求余弦函数的最值从而求得值域的问题,是中档题.

练习册系列答案
相关题目
函数f(x)=
的定义域为( )
| 1 | ||
|
| A、(0,3) |
| B、(0,3] |
| C、(3,+∞) |
| D、[3,+∞) |
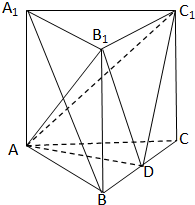 如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点