题目内容
设方程sin4x=0的解集为M，方程cos2x=1的解集为P，则M与P之间的关系是（ ）
| A、P?M | B、M?P |
| C、M=P | D、M∩P=∅ |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：由三角函数的知识可求出集合M、P，从而确定集合的关系．
解答：
解：∵sin4x=0，∴4x=kπ，
即M={x|x=
，k∈Z}；
∵cos2x=1，∴2x=2kπ，
即P={x|x=kπ，k∈Z}；
则P?M，
故选A．
即M={x|x=
| kπ |
| 4 |
∵cos2x=1，∴2x=2kπ，
即P={x|x=kπ，k∈Z}；
则P?M，
故选A．
点评：本题考查了集合的化简与集合的运算，属于基础题．
练习册系列答案
相关题目
在三棱锥P-ABC中，平面PBC⊥平面ABC，AB=AC，E，F分别为BC，BP的中点，求证：（1）直线EF∥平面PAC；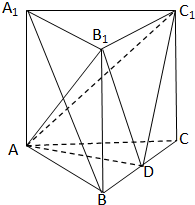
如图，三棱柱中ABC-A1B1C1，侧棱CC1⊥底面ABC，且侧棱和底面边长均为2，D是BC的中点