题目内容
 如图,在Rt△ABC中,AC=1,BC=x,D为斜边AB的中点.将△BCD沿直线CD翻折.若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是
如图,在Rt△ABC中,AC=1,BC=x,D为斜边AB的中点.将△BCD沿直线CD翻折.若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:由题意得,AD=CD=BD═
,BC=x,取BC中点E,翻折前,DE=
,AC=
,翻折后,CB⊥AD,BC⊥AE,DE⊥BC,AB=AC=1,AE=
,AD=
,由此能求出x的取值范围.
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
1-
|
| ||
| 2 |
解答:
解:由题意得,AD=CD=BD═
,BC=x,取BC中点E,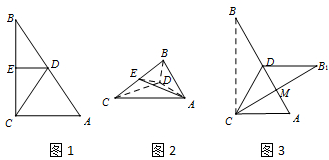 翻折前,在图1中,连接DE,CD,则DE=
翻折前,在图1中,连接DE,CD,则DE=
,AC=
,
翻折后,在图2中,此时 CB⊥AD.
∵BC⊥DE,BC⊥AD,∴BC⊥平面ADE,
∴BC⊥AE,DE⊥BC,
又BC⊥AE,E为BC中点,∴AB=AC=1,
∴AE=
,AD=
,
在△ADE中:①
+
>
,②
<
+
,③x>0,
由①②③,得0<x<
.
如图3,翻折后,当△B1CD与△ACD在一个平面上,
AD与B1C交于M,且AD⊥B1C,AD=B1D=CD=BD,∠CBD=∠BCD=∠B1CD,
又∠CBD+∠BCD+∠B1CD=90°,
∴∠CBD=∠BCD=∠B1CD=30°,
∴∠A=60°,BC=ACtan60°,此时x=1×
=
,
综上,x的取值范围为(0,
].
故答案为:(0,
].
| ||
| 2 |
 翻折前,在图1中,连接DE,CD,则DE=
翻折前,在图1中,连接DE,CD,则DE=| 1 |
| 2 |
| 1 |
| 2 |
翻折后,在图2中,此时 CB⊥AD.
∵BC⊥DE,BC⊥AD,∴BC⊥平面ADE,
∴BC⊥AE,DE⊥BC,
又BC⊥AE,E为BC中点,∴AB=AC=1,
∴AE=
1-
|
| ||
| 2 |
在△ADE中:①
| ||
| 2 |
| 1 |
| 2 |
1-
|
| ||
| 2 |
| 1 |
| 2 |
1-
|
由①②③,得0<x<
| 3 |
如图3,翻折后,当△B1CD与△ACD在一个平面上,
AD与B1C交于M,且AD⊥B1C,AD=B1D=CD=BD,∠CBD=∠BCD=∠B1CD,
又∠CBD+∠BCD+∠B1CD=90°,
∴∠CBD=∠BCD=∠B1CD=30°,
∴∠A=60°,BC=ACtan60°,此时x=1×
| 3 |
| 3 |
综上,x的取值范围为(0,
| 3 |
故答案为:(0,
| 3 |
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知A、B是抛物线y2=4p上不同的两点,且直线AB的倾斜角为锐角,F为抛物线的焦点,且
=-4
,则直线AB的斜率为( )
| FA |
| FB |
A、
| ||
B、
| ||
C、
| ||
D、
|
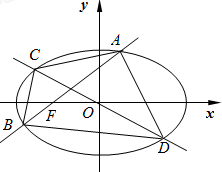 如图,已知椭圆E:
如图,已知椭圆E: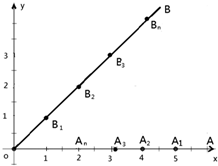 平面直角坐标系中,O为原点,射线OA与x轴正半轴重合,射线OB是第一象限角平分线.在OA上有点列A1,A2,A3,…,An,…,在OB上有点列B1,B2,B3,…,Bn,…已知
平面直角坐标系中,O为原点,射线OA与x轴正半轴重合,射线OB是第一象限角平分线.在OA上有点列A1,A2,A3,…,An,…,在OB上有点列B1,B2,B3,…,Bn,…已知