题目内容
已知平面α，β是两个不重合的平面，其法向量分别为n1，n2，给出下列结论：
①若n1∥n2，则α∥β；
②若n1∥n2，则α⊥β；
③若n1•n2=0，则α⊥β；
④若n1•n2=0，则α∥β．
其中正确的是（ ）
①若n1∥n2，则α∥β；
②若n1∥n2，则α⊥β；
③若n1•n2=0，则α⊥β；
④若n1•n2=0，则α∥β．
其中正确的是（ ）
| A、①③ | B、①② | C、②③ | D、②④ |
考点：命题的真假判断与应用
专题：空间位置关系与距离,简易逻辑
分析：直接利用平面的法向量垂直于平面逐一分析四个命题得答案．
解答：
解：已知平面α，β是两个不重合的平面，其法向量分别为
，
，
①若
∥
，则α∥β，命题①正确；
②若
∥
，则α∥β，∴α⊥β不正确，命题②错误；
③若
•
=0，则
⊥
，则α⊥β，命题③正确；
④若
•
=0，则
⊥
，∴α∥β不正确，命题④错误．
∴正确的命题是①②．
故选：A．
| n1 |
| n2 |
①若
| n1 |
| n2 |
②若
| n1 |
| n2 |
③若
| n1 |
| n2 |
| n1 |
| n2 |
④若
| n1 |
| n2 |
| n1 |
| n2 |
∴正确的命题是①②．
故选：A．
点评：本题考查了命题的真假判断与应用，考查了利用平面法向量判断判断两个平面间的位置关系，是基础题．
练习册系列答案
相关题目
已知f（x）=x2-2|x|，则满足f[f（x）]=-
的实数x的个数为（ ）
| 1 |
| 2 |
| A、2 | B、4 | C、6 | D、8 |
如图，在Rt△ABC中，AC=1，BC=x，D为斜边AB的中点．将△BCD沿直线CD翻折．若在翻折过程中存在某个位置，使得CB⊥AD，则x的取值范围是在正三棱锥P-ABC中，三条侧棱两两互相垂直，侧棱长为a，则点P到平面ABC的距离为（ ）
| A、a | ||||
B、
| ||||
C、
| ||||
D、
|
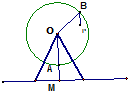某公园的摩天轮观览车主架示意图如图所示，其中O为轮轴中心，距地面32m（即OM长），巨轮半径为30m，AM=BP=2m，巨轮逆时针旋转且12分钟转动一圈．若点M为P的初始位置（O，A，M共线），经过t分钟，该吊舱P距地面的高度为h（t），则h（t）=光线从点A（-3，5）射到x轴上，经反射以后经过点B（2，10），则光线从A到B的距离为（ ）
A、5
| ||
B、2
| ||
C、5
| ||
D、10
|