Question

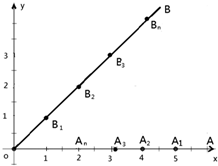平面直角坐标系中，O为原点，射线OA与x轴正半轴重合，射线OB是第一象限角平分线．在OA上有点列A₁，A₂，A₃，…，A_n，…，在OB上有点列B₁，B₂，B₃，…，B_n，…已知

OAn+1

=

4

5

OAn

，A₁（5，0），|

OB1

|=

2

，|

OBn+1

|=|

OBn

|+

2

．
（1）求点A₂，B₁的坐标；
（2）求

OAn

，

OBn

的坐标；
（3）求△A_nOB_n面积的最大值，并说明理由．

Answer 1

考点：数列的应用

专题：等差数列与等比数列

分析：（1）由

OA2

=

4

5

OA1

和A₁（5，0）可求A₂（4，0），由射线OB是第一象限角平分线和|

OB1

|=

2

，利用向量模的公式可求B₁（1，1）．
（2）设

OAn

=(xn，0)，

OAn+1

=

4

5

OAn

，得(xn+1，0)=

4

5

(xn，0)，⇒xn+1=

4

5

xn⇒{x_n}成等比数列，又x1=5，q=

4

5

，得xn=5•(

4

5

)n-1，进而得到

OAn

=(5•(

4

5

)n-1，0)；设

OBn

=(yn，yn)，yn＞0，得|

OBn

|=

2

yn，由|

OBn+1

|=|

OBn

|+

2

，得y_n+1=y_n+1得{y_n}是等差数列，可求得y_n=1+（n-1）=n，进而求得

OBn

=(n，n)；（3）由S△AnOBn=

1

2

|

OAn

||

OBn

|sin

π

4

，可得S△AnOBn=

1

2

•5•(

4

5

)n-1•

2

n•

2

2

=

25n

8

•(

4

5

)n，利用换元法设tn=

25n

8

•(

4

5

)n，当n≥2时，tn-tn-1=

25n

8

•(

4

5

)n-

25(n-1)

8

•(

4

5

)n-1可知1≤n≤4时，{t_n}是递增数列，n≥6时，{t_n}是递减数列，即t₁＜t₂＜t₃＜t₄=t₅＞t₆＞t₇＞…＞t_n＞…进而求得(S△AnOBn)max=t4=t5=

128

25

．

解答： 解：（1）

OA2

=

4

5

OA1

=

4

5

(5，0)=(4，0)，A₂（4，0），（2分）
设B₁（x，x），x＞0，由|

OB1

|=

2

，得

x2+y2

=

2

，
x=1，∴B₁（1，1）．
（2）设

OAn

=(xn，0)，则(xn+1，0)=

4

5

(xn，0)，⇒xn+1=

4

5

xn，{x_n}成等比数列，
x1=5，q=

4

5

，xn=5•(

4

5

)n-1，
∴

OAn

=(5•(

4

5

)n-1，0)．（6分）
设

OBn

=(yn，yn)，yn＞0，|

OBn

|=

2

yn由|

OBn+1

|=|

OBn

|+

2

⇒yn+1=yn+1，
∴{y_n}是等差数列 （8分）y_n=1+（n-1）=n，
∴

OBn

=(n，n)．（9分）
（3）S△AnOBn=

1

2

|

OAn

||

OBn

|sin

π

4

=

1

2

•5•(

4

5

)n-1•

2

n•

2

2

=

25n

8

•(

4

5

)n，（11分）
设tn=

25n

8

•(

4

5

)n，当n≥2时，tn-tn-1=

25n

8

•(

4

5

)n-

25(n-1)

8

•(

4

5

)n-1=

125

128

•(

4

5

)n(5-n)，
∴1≤n≤4时，{t_n}是递增数列，n≥6时，{t_n}是递减数列，t₁＜t₂＜t₃＜t₄=t₅＞t₆＞t₇＞…＞t_n＞…，
∴(S△AnOBn)max=t4=t5=

128

25

．

点评：本题考查点A₂，B₁的坐标的求法，考

OAn

，

OBn

的坐标的求法，考查△A_nOB_n面积的最大值的求法，是中档题，解题时要认真审题，注意数列和向量知识的综合应用．