题目内容
设f(x)=ax2+bx+c(a≠0),f′(x)=2x+2.且方程f(x)=0有两个相等的实根.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积.
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:(1)求导函数,结合f′(x)=2x+2,确定a,b的值,根据方程f(x)=0有两个相等的实根,求出c的值,可得结论;
(2)利用积分表示面积,再求积分即可.
(2)利用积分表示面积,再求积分即可.
解答:
解:(1)由f(x)=ax2+bx+c,得f′(x)=2ax+b,
∵f′(x)=2x+2,∴a=1,b=2,∴f(x)=x2+2x+c,
∵方程f(x)=0有两个相等的实根,
∴4-4c=0,∴c=1,
∴f(x)=x2+2x+1;
(2)由x2+2x+1=0,可得x=-1,所以y=f(x)的图象与两坐标轴所围成图形的面积S=
(x2+2x+1)dx=(
x3+x2+x)
=
.
∵f′(x)=2x+2,∴a=1,b=2,∴f(x)=x2+2x+c,
∵方程f(x)=0有两个相等的实根,
∴4-4c=0,∴c=1,
∴f(x)=x2+2x+1;
(2)由x2+2x+1=0,可得x=-1,所以y=f(x)的图象与两坐标轴所围成图形的面积S=
| ∫ | 0 -1 |
| 1 |
| 3 |
| | | 0 -1 |
| 1 |
| 3 |
点评:本题考查导数知识的运用,考查定积分,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
曲线
+
=1与曲线
+
=1(k<3)的( )
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4-k |
| y2 |
| 3-k |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
 如图是容量为100的样本的频率分布直方图,则样本数据在[14,18)内的频率和频数分别是( )
如图是容量为100的样本的频率分布直方图,则样本数据在[14,18)内的频率和频数分别是( )| A、0.24,24 |
| B、0.08,8 |
| C、0.32,32 |
| D、0.36,36 |
 某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表: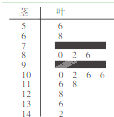 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: